已知.如图所示.点E.F分别为任意四边形ABCD对边AB.CD的中点.求证:$\overrightarrow{EF}$=$\frac{1}{2}$($\overrightarrow{AC}$+$\overrightarrow{BD}$)．题目和参考答案——青夏教育精英家教网—

题目内容

13．

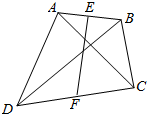已知，如图所示，点E、F分别为任意四边形ABCD对边AB、CD的中点，求证：$\overrightarrow{EF}$=$\frac{1}{2}$（$\overrightarrow{AC}$+$\overrightarrow{BD}$）．

分析借助于平面向量的三角形法则即可整理出来．

解答解：∵$\overrightarrow{AC}+\overrightarrow{BD}$=$（\overrightarrow{AB}+\overrightarrow{BC}）+（\overrightarrow{BC}+\overrightarrow{CD）}$=$\overrightarrow{AB}$+2$\overrightarrow{BC}$+$\overrightarrow{CD}$=2$\overrightarrow{EB}$+2$\overrightarrow{BC}$+2$\overrightarrow{CF}$，
$\overrightarrow{EF}$=$\overrightarrow{EB}+\overrightarrow{BC}+\overrightarrow{CF}$，
∴$\overrightarrow{EF}$=$\frac{1}{2}$（$\overrightarrow{AC}+\overrightarrow{BD}$）．

点评本题考查了平面向量加法的几何意义，属于基础题．

练习册系列答案

	A．	充分非必要条件		B．	必要非充分条件
	C．	充要条件		D．	既非充分也非必要条件

4．设z₁，z₂是复数，则下列命题中的假命题是（　　）

	A．	若\|z₁\|=\|z₂\|，则${z_1}^2={z_2}^2$		B．	若${z_1}=\overline{z_2}$，则$\overline{z_1}={z_2}$
	C．	若\|z₁\|=\|z₂\|，则${z_1}•\overline{z_1}={z_2}•\overline{z_2}$		D．	若\|z₁-z₂\|=0，则$\overline{z_1}=\overline{z_2}$

1．已知函数$f（x）=\sqrt{{x^2}+4}+\frac{1}{{\sqrt{{x^2}+4}}}$，则函数y=f（x）的最小值为$\frac{5}{2}$．

8．

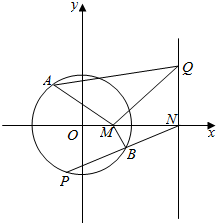如图，自点M（1，0）引直线交椭圆$\frac{{x}^{2}}{4}$+y²=1于A，B两点，直线l：x=4与x轴交于点N，设点A关于x轴的对称点为P（异于点B）．
（1）求证：P、B、N三点共线；
（2）过点A作PB的平行线交直线l：x=4于点Q，记△AQM、△QMN、△BMN的面积分别为S₁、S₂、S₃，是否存在常数λ，使得S₂²=λS₁S₃？若存在，请求出λ的值：若不存在，请说明理由．

18．已知α∈（$\frac{π}{2}$，π），tan（α+$\frac{π}{4}$）=$\frac{1}{7}$，则sinα+cosα=-$\frac{1}{5}$．

5．若x²+2（m-1）x+2m+6＞0在x∈[0，2]上总成立，求实数m的范围．

2．已知函数f（x）=x³-3x．
（1）计算：函数y=f（x）的零点；
（2）证明：函数f（x）在[1，+∞）上是单调递增函数．

3．下列各角中，和-40°终边相同的角是（　　）

试题分类