题目内容
1.已知函数$f(x)=\sqrt{{x^2}+4}+\frac{1}{{\sqrt{{x^2}+4}}}$,则函数y=f(x)的最小值为$\frac{5}{2}$.分析 先换元t=$\sqrt{x^2+4}$∈[2,+∞),原函数可化为g(t)=t+$\frac{1}{t}$,t∈[2,+∞),再根据双勾函数的图象和性质求出f(x)的最小值.
解答 解:令t=$\sqrt{x^2+4}$∈[2,+∞),
则$f(x)=\sqrt{{x^2}+4}+\frac{1}{{\sqrt{{x^2}+4}}}$=t+$\frac{1}{t}$,
记g(t)=t+$\frac{1}{t}$,t∈[2,+∞),
根据双勾函数的性质,g(t)在(0,1)上单调递减,在(1,+∞)上单调递增,
所以,当t∈[2,+∞)时,g(t)单调递增,
因此,g(t)min=g(2)=2+$\frac{1}{2}$=$\frac{5}{2}$,
即函数f(x)的最小值为$\frac{5}{2}$,
故答案为:$\frac{5}{2}$.
点评 本题主要考查了应用函数的单调性求函数的最值,涉及双勾函数的图象和性质,属于中档题.

练习册系列答案
相关题目
9.已知函数f(lgx)定义域是[0.1,100],则函数$f(\frac{x}{2})$的定义域是( )
| A. | [-1,2] | B. | [-2,4] | C. | [0.1,100] | D. | $[{-\frac{1}{2},1}]$ |
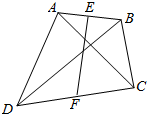 已知,如图所示,点E、F分别为任意四边形ABCD对边AB、CD的中点,求证:$\overrightarrow{EF}$=$\frac{1}{2}$($\overrightarrow{AC}$+$\overrightarrow{BD}$).
已知,如图所示,点E、F分别为任意四边形ABCD对边AB、CD的中点,求证:$\overrightarrow{EF}$=$\frac{1}{2}$($\overrightarrow{AC}$+$\overrightarrow{BD}$).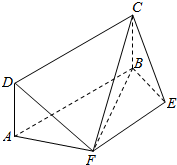 如图,矩形ABCD所在的平面与平面ABEF互相垂直,ABEF是等腰梯形,AB∥EF,AB=2,AD=AF=EF=BE=1.
如图,矩形ABCD所在的平面与平面ABEF互相垂直,ABEF是等腰梯形,AB∥EF,AB=2,AD=AF=EF=BE=1.