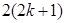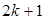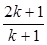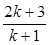题目内容
已知函数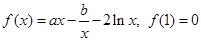
(Ⅰ)若函数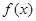 在其定义域上为单调函数,求
在其定义域上为单调函数,求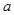 的取值范围;
的取值范围;
(Ⅱ)若函数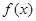 的图像在
的图像在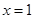 处的切线的斜率为0,
处的切线的斜率为0,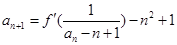 ,已知
,已知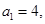 求证:
求证: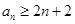
(Ⅲ)在(2)的条件下,试比较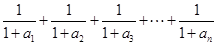 与
与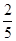 的大小,并说明理由.
的大小,并说明理由.
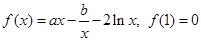
(Ⅰ)若函数
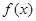 在其定义域上为单调函数,求
在其定义域上为单调函数,求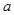 的取值范围;
的取值范围;(Ⅱ)若函数
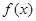 的图像在
的图像在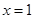 处的切线的斜率为0,
处的切线的斜率为0,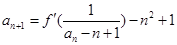 ,已知
,已知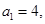 求证:
求证: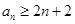
(Ⅲ)在(2)的条件下,试比较
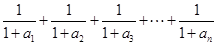 与
与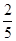 的大小,并说明理由.
的大小,并说明理由. (Ⅰ)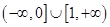 ;(Ⅱ)略;(Ⅲ)
;(Ⅱ)略;(Ⅲ)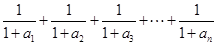 <
<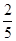 .
.
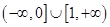 ;(Ⅱ)略;(Ⅲ)
;(Ⅱ)略;(Ⅲ)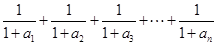 <
<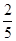 .
.试题分析:(Ⅰ)利用导数求解单调性,把恒成立转化为最值;(Ⅱ)可用数学归纳法来证明
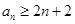 ;(Ⅲ)通过放缩法来解决
;(Ⅲ)通过放缩法来解决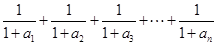 与
与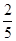 的大小比较问题.
的大小比较问题.试题解析:(Ⅰ) ∵f(1)="a-b=0" ∴a=b
∴
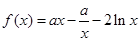
∴
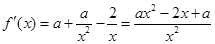
要使函数
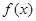 在其定义域上为单调函数,则在定义域(0,+∞)内
在其定义域上为单调函数,则在定义域(0,+∞)内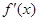 恒大于等于0或恒小于等于0,
恒大于等于0或恒小于等于0,当a=0时,
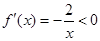 在(0,+∞)内恒成立;
在(0,+∞)内恒成立;当a>0时,
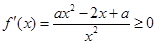 恒成立,则
恒成立,则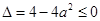 ∴
∴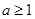
当a<0时,
 恒成立
恒成立∴a的取值范围是:
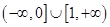 5分
5分(Ⅱ)
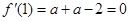 ∴a=1 则:
∴a=1 则: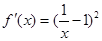
于是
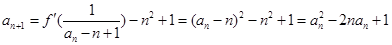
用数学归纳法证明
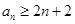 如下:
如下:当n=1时,
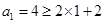 ,不等式成立;
,不等式成立;假设当n=k时,不等式
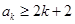 成立,即
成立,即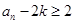 也成立,
也成立,当n=k+1时,
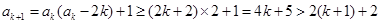
所以当n=k+1时不等式成立,
综上得对所有
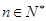 时,都有
时,都有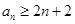 10分
10分(Ⅲ)由(2)得
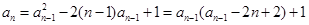
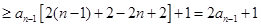
于是
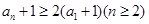
所以
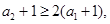
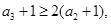 ,
,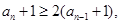
累称得:
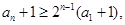 则
则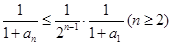
所以
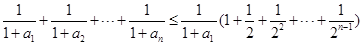
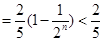 13分
13分
练习册系列答案
相关题目
 +
+ +…+
+…+ =
= (n∈N*).
(n∈N*). 当
当 时,试猜想
时,试猜想 的值,并用数学归纳法给予证明。
的值,并用数学归纳法给予证明。 (n∈N*),则a3=________,a1·a2·a3·…·a2014=________.
(n∈N*),则a3=________,a1·a2·a3·…·a2014=________.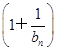 (其中a>0且a≠1).记Sn是数列{an}的前n项和,试比较Sn与
(其中a>0且a≠1).记Sn是数列{an}的前n项和,试比较Sn与 logabn+1的大小,并证明你的结论.
logabn+1的大小,并证明你的结论.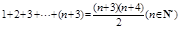 时,第一步验证
时,第一步验证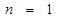 时,左边应取的项是
时,左边应取的项是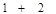
 对任意实数x 、y都有
对任意实数x 、y都有 ,
, 的值;
的值; ,求
,求 、
、 、
、 的值;
的值;
 的表达式,并用数学归纳法加以证明。
的表达式,并用数学归纳法加以证明。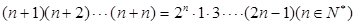 ,从“k到k+1”左端需增乘的代数式为( )
,从“k到k+1”左端需增乘的代数式为( )