题目内容
10.设变量x,y满足约束条件$\left\{\begin{array}{l}{x-y+2≥0}\\{2x+3y-6≥0}\\{3x+2y-9≤0}\end{array}\right.$,则目标函数z=2x-y的最大值是( )| A. | -2 | B. | 2 | C. | -6 | D. | 6 |
分析 先根据约束条件画出可行域,再利用几何意义求最值,z=2x-y表示直线在y轴上的截距,只需求出可行域直线在y轴上的截距最小值即可.
解答  解:约束条件件$\left\{\begin{array}{l}{x-y+2≥0}\\{2x+3y-6≥0}\\{3x+2y-9≤0}\end{array}\right.$,不等式组表示的平面区域如图所示,
解:约束条件件$\left\{\begin{array}{l}{x-y+2≥0}\\{2x+3y-6≥0}\\{3x+2y-9≤0}\end{array}\right.$,不等式组表示的平面区域如图所示,
当直线z=2x-y过点A时,z取得最大值,
由$\left\{\begin{array}{l}{2x+3y-6=0}\\{3x+2y-9=0}\end{array}\right.$,可得A(3,0)时,
在y轴上截距最小,此时z取得最大值6.
故选:D
点评 本题主要考查了简单的线性规划,以及利用几何意义求最值,属于基础题.

练习册系列答案
相关题目
20.执行如图所示的程序图,则输出的S值为( )


| A. | 4 | B. | 3 | C. | -2 | D. | -3 |
1.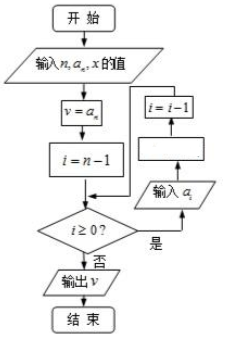 我国南宋时期的数学家秦九韶在他的著作《数书九章》中提出了计算多项式f(x)=anxn+an-1xn-1+…+a1x+a0的值的秦九韶算法,即将f(x)改写成如下形式:f(x)=(…((anx+an-1)x+an-2)x+…+a1)x+a0,首先计算最内层一次多项式的值,然后由内向外逐层计算一次多项式的值,这种算法至今仍是比较先进的算法,将秦九韶算法用程序框图表示如图,则在空白的执行框内应填入( )
我国南宋时期的数学家秦九韶在他的著作《数书九章》中提出了计算多项式f(x)=anxn+an-1xn-1+…+a1x+a0的值的秦九韶算法,即将f(x)改写成如下形式:f(x)=(…((anx+an-1)x+an-2)x+…+a1)x+a0,首先计算最内层一次多项式的值,然后由内向外逐层计算一次多项式的值,这种算法至今仍是比较先进的算法,将秦九韶算法用程序框图表示如图,则在空白的执行框内应填入( )
 我国南宋时期的数学家秦九韶在他的著作《数书九章》中提出了计算多项式f(x)=anxn+an-1xn-1+…+a1x+a0的值的秦九韶算法,即将f(x)改写成如下形式:f(x)=(…((anx+an-1)x+an-2)x+…+a1)x+a0,首先计算最内层一次多项式的值,然后由内向外逐层计算一次多项式的值,这种算法至今仍是比较先进的算法,将秦九韶算法用程序框图表示如图,则在空白的执行框内应填入( )
我国南宋时期的数学家秦九韶在他的著作《数书九章》中提出了计算多项式f(x)=anxn+an-1xn-1+…+a1x+a0的值的秦九韶算法,即将f(x)改写成如下形式:f(x)=(…((anx+an-1)x+an-2)x+…+a1)x+a0,首先计算最内层一次多项式的值,然后由内向外逐层计算一次多项式的值,这种算法至今仍是比较先进的算法,将秦九韶算法用程序框图表示如图,则在空白的执行框内应填入( )| A. | v=vx+ai | B. | v=v(x+ai) | C. | v=aix+v | D. | v=ai(x+v) |
18.某几何体的三视图如图所示,则其体积为( )
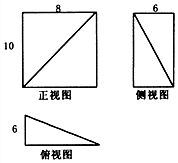

| A. | 80 | B. | 160 | C. | 240 | D. | 480 |
5.执行如图所示的程序框图,若输入p=2017,则输出i的值为( )
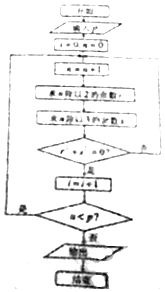

| A. | 335 | B. | 336 | C. | 337 | D. | 338 |
15.已知i是虚数单位,则$\frac{1+i}{1-i}$=( )
| A. | 1 | B. | -1 | C. | i | D. | -i |
10.如图,输入n=5时,则输出的S=( )
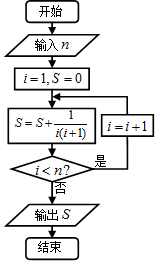

| A. | $\frac{3}{4}$ | B. | $\frac{4}{5}$ | C. | $\frac{5}{6}$ | D. | $\frac{6}{7}$ |