Question

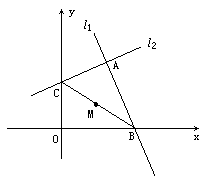
过定点A(a，b)任作互相垂直的两直线l₁与l₂，且l₁与x轴相交于M点，l₂与y轴相交于N点，求线段MN中点P的轨迹方程.

Answer 1

解法一:设M(x₁，0)，N(0，y₁)，P(x，y).

∵P点为线段MN的中点，

∴∴                                                                                                    ①

又∵l₁⊥l₂，∴|AM|²＋|AN|²＝|MN|²,

即(x₁－a)²＋(0－b)²＋(y₁－b)²＋(0－a)²＝(x₁－0)²＋(y₁－0)²,

即(x₁－a)²＋a²＋(y₁－b)²＋b²＝x₁²＋y₁².                                                                     ②

把①代入②化简得2ax＋2by－a²－b²＝0，即为P点的轨迹方程.

解法二:设P(x，y).

①当AM与x轴不垂直时，∵P为MN中点，∴M(2x，0)，N(0，2y).

又k_AM＝，k_BN＝，l₁⊥l₂,∴·＝－1.

化简得2ax＋2by－a²－b²＝0.                                                                                    ①

②当AM⊥x轴时，AM的斜率不存在，此时MN中点坐标(，)满足方程①.

综上所述，得P点的轨迹方程为2ax＋2by－a²－b²＝0.