题目内容
18.已知cos(α-$\frac{β}{2}$)=-$\frac{1}{9}$,sin($\frac{α}{2}$-β)=$\frac{2}{3}$,且0<β<$\frac{π}{2}$<α<π,则sin$\frac{α+β}{2}$=$\frac{22}{27}$.分析 利用同角三角函数的基本关系求得sin(α-$\frac{β}{2}$)和cos($\frac{α}{2}$-β)的值,再利用两角差的正弦公式求得sin$\frac{α+β}{2}$的值.
解答 解:∵cos(α-$\frac{β}{2}$)=-$\frac{1}{9}$,sin($\frac{α}{2}$-β)=$\frac{2}{3}$,且0<β<$\frac{π}{2}$<α<π,
∴α-$\frac{β}{2}$∈($\frac{π}{2}$,π),sin(α-$\frac{β}{2}$)=$\sqrt{{1-cos}^{2}(α-\frac{β}{2})}$=$\frac{4\sqrt{5}}{9}$; $\frac{α}{2}$-β∈(0,$\frac{π}{2}$),cos($\frac{α}{2}$-β)=$\sqrt{{1-sin}^{2}(\frac{α}{2}-β)}$=$\frac{\sqrt{5}}{3}$.
则sin$\frac{α+β}{2}$=sin[(α-$\frac{β}{2}$)-( $\frac{α}{2}$-β)]=sin(α-$\frac{β}{2}$)cos( $\frac{α}{2}$-β)-cos(α-$\frac{β}{2}$)sin($\frac{α}{2}$-β)
=$\frac{4\sqrt{5}}{9}$•$\frac{\sqrt{5}}{3}$+$\frac{1}{9}$•$\frac{2}{3}$=$\frac{22}{27}$.
点评 本题主要考查同角三角函数的基本关系、两角差的正弦公式的应用,属于基础题.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
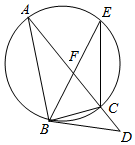 如图,△ABC为圆的内接三角形,∠ABC的平分线BF交圆于点E,过点B作圆的切线交AC的延长线于点D
如图,△ABC为圆的内接三角形,∠ABC的平分线BF交圆于点E,过点B作圆的切线交AC的延长线于点D