题目内容
19.(1-x)5(3+2x)9=a0(x+1)14+a1(x+1)13+…+a13(x+1)+a14,求:(1)a0+a1+…+a14的值;
(2)a1+a3+…a13的值.
分析 (1)令x=0,可得:(1-0)5(3+2×0)9=a0(0+1)14+a1(0+1)13+…+a13(0+1)+a14,化简即可得出.
(2)令x=-2可得:a0-a1-…-a14=-35.又a0+a1+…+a14=39.即可得出.
解答 解:(1)令x=0,可得:(1-0)5(3+2×0)9=a0(0+1)14+a1(0+1)13+…+a13(0+1)+a14,
∴a0+a1+…+a14=39.
(2)令x=-2可得:(1+2)5(3-4)9=a0(-2+1)14+a1(-2+1)13+…+a13(-2+1)+a14,
∴a0-a1-…-a14=-35.
又a0+a1+…+a14=39.
∴2(a1+a3+…a13)=39+35,
∴a1+a3+…a13=38+34.
点评 本题考查了二项式定理的应用,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
14.执行如图所示的程序框图,输出的n为( )


| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
11.已知命题p:若α为第一象限角,β为第二象限角,则α<β;命题q:在等比数列{an}中,若a1<a2,则数列{an}为递减数列,下列命题为真命题的是( )
| A. | p∧q | B. | (¬p)∧(¬q) | C. | (¬p)∧q | D. | p∨q |
9.若$\frac{π}{4}$<θ<$\frac{θ}{2}$,则$\sqrt{1-sin2θ}$的值为( )
| A. | cosθ-sinθ | B. | sinθ-cosθ | C. | $\sqrt{2}$sinθ | D. | $\sqrt{2}$cosθ |
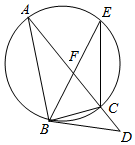 如图,△ABC为圆的内接三角形,∠ABC的平分线BF交圆于点E,过点B作圆的切线交AC的延长线于点D
如图,△ABC为圆的内接三角形,∠ABC的平分线BF交圆于点E,过点B作圆的切线交AC的延长线于点D