题目内容
13、f(x)=(x2-3)ex(e为自然对数的底数)的最小值是
-2e
.分析:利用两个乘积函数的求导法则求出函数f(x)的导函数,再根据导函数判断单调性求函数最值.
解答:解:f(x)=(x2-3)ex
∴f′(x)=(x2-3)ex+2x•ex
令f′(x)=(x2-3)ex+2x•ex ;;=0
∴x=-3或x=1
∴f(x)的单调递增区间为(-∞,-3)和(1,+∞)∴f(x)的单调递减区间为(-3,1)
且函数在(-∞,-3)上f(x)>0恒成立
∴f(x)min=f(1)=-2e
故答案为:-2e
∴f′(x)=(x2-3)ex+2x•ex
令f′(x)=(x2-3)ex+2x•ex ;;=0
∴x=-3或x=1
∴f(x)的单调递增区间为(-∞,-3)和(1,+∞)∴f(x)的单调递减区间为(-3,1)
且函数在(-∞,-3)上f(x)>0恒成立
∴f(x)min=f(1)=-2e
故答案为:-2e
点评:本题考查函数的导数研究函数的方法,解题的关键是要对两个函数乘积的求导公式熟练掌握,属于基础题.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
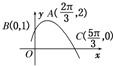 已知函数f(x)的部分图象如图所示,则f(x)的解析式可能为( )
已知函数f(x)的部分图象如图所示,则f(x)的解析式可能为( )A、f(x)=2cos(
| ||||
B、f(x)=
| ||||
C、f(x)=2sin(
| ||||
D、f(x)=2sin(4x+
|
已知函数f(x)=Asin(ωx+φ)的部分图象如图所示,则f(x)的解析式可能为( )
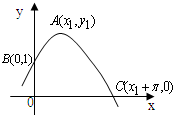

A、f(x)=2sin(
| ||||
B、f(x)=
| ||||
C、f(x)=2cos(
| ||||
D、f(x)=2sin(4x+
|