题目内容
已知x，a∈R，a＞1，直线y=x与函数f（x）=logax有且仅有一个公共点，则a= ；公共点坐标是 ．
【答案】分析：构造新函数g（x）=logax-x，求导函数，确定函数的单调性与最大值，利用直线y=x与函数f（x）=logax有且仅有一个公共点，即可求得结论．
解答：解：构造新函数g（x）=logax-x，g′（x）=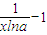
，
令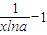
=0，有x=
，
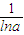因为a＞1，当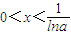
时，g′（x）＞0；当
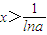时，g′（x）＜0
所以，g（x）=logax-x在x=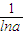
处有最大值g（
），
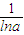当g（
）时，直线y=x与函数f（x）=logax有且仅有一个公共点，即loga（
）=
，
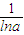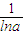∴ln（lna）=-1，lna=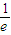
，∴
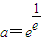
则y=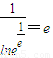
，即公共点坐标是（a，e），
故答案为：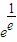
，（a，e）．
点评：本题考查导数和函数零点等知识解决问题的能力，考查学生创新意识、运用数学知识解决问题的能力和计算能力．
解答：解：构造新函数g（x）=logax-x，g′（x）=
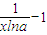，令
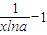=0，有x=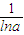，因为a＞1，当
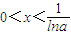时，g′（x）＞0；当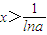时，g′（x）＜0所以，g（x）=logax-x在x=
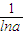处有最大值g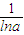（），当g（
）时，直线y=x与函数f（x）=logax有且仅有一个公共点，即loga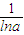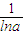（）=，∴ln（lna）=-1，lna=
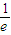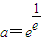
，∴则y=
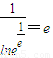，即公共点坐标是（a，e），故答案为：
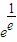，（a，e）．点评：本题考查导数和函数零点等知识解决问题的能力，考查学生创新意识、运用数学知识解决问题的能力和计算能力．
练习册系列答案
阅读快车系列答案
相关题目
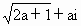(a∈R且a≥－
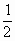)，若z＝x－|x|＋(1－i)分别为实数、虚数、纯虚数和在第二象限时，求实数a的取值．
+ai(a∈R且a≥-
),若z=x-|x|+(1-i):(1)z为纯虚数;(2)与z对应的点在第二象限;求实数a的值.
+ai(a∈R且a≥-
),若z=x-|x|+(1-i)分别为实数、虚数、纯虚数和在第二象限时，求实数a的值.