题目内容
已知集合A＝{x|x2－2x－3≤0}，B＝{x|m－2≤x≤m＋2，m∈R}．
(1)若A∪B＝A，求实数m的取值；
(2)若A∩B＝{x|0≤x≤3}，求实数m的值；
(3)若A⊆∁RB，求实数m的取值范围．
解：A＝{x|－1≤x≤3}，B＝{x|m－2≤x≤m＋2}
(1)∵A∪B＝A，∴B⊆A，如图
有：
，∴m＝1.
(2)∵A∩B＝{x|0≤x≤3}∴
，∴m＝2.
(3)∁RB＝{x|x<m－2或x>m＋2}．
∵A⊆∁RB ∴m－2>3或m＋2<－1，
∴m>5或m<－3.
练习册系列答案
阅读快车系列答案
相关题目
,
(
两两互相垂直)，那么
= 。
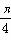，则tan α＝1”的逆否命题为假命题；
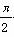＋kπ(k∈Z)”是“函数y＝sin(2x＋φ)为偶函数”的充要条件；
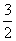”；命题q：“若sin α>sin β，则α>β ”，那么(綈p)∧q为真命题．
定义域相同的函数为( )
B．y＝
>3a2，则a的取值范围是________．
＝1.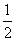
x2＋bx(b，c∈R，c≠0)，且x＝1为f(x)的极值点．