题目内容
12.已知f(x)是R奇函数,对x∈R都有f(x+4)=f(x)+f(2)成立,若f(1)=2,则f(2015)等于-2.分析 令x=-2,可得f(2)=f(-2)+f(2),得出f(2)=0,f(x+4)=f(x),利用周期性求解即可.
解答 解:对x∈R都有f(x+4)=f(x)+f(2)成立,∴f(2)=f(-2)+f(2),
∴f(-2)=0,f(2)=0,
∴f(x+4)=f(x),
∴f(x)的周期为4,
∴f(2015)=f(3)=f(-1)=-f(1)=-2.
点评 考查了抽象函数的周期性及奇偶性的综合.属于基础题型,应熟练掌握.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
4.命题p:“|a|+|b|≤1”;命题q:“对任意的x∈R,不等式asinx+bcosx≤1恒成立”,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
1.函数f(x)=ln(x2+2)-ex-1的图象可能是( )
| A. |  | B. | 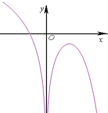 | C. | 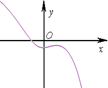 | D. |  |
