题目内容
用数学归纳法证明等式1+2+3+…+(n+3)=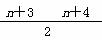 (n∈N*)时,第一步验证
(n∈N*)时,第一步验证
n=1时,左边应取的项是( )
A.1 B.1+2
C.1+2+3 D.1+2+3+4
D

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
题目内容
用数学归纳法证明等式1+2+3+…+(n+3)=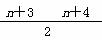 (n∈N*)时,第一步验证
(n∈N*)时,第一步验证
n=1时,左边应取的项是( )
A.1 B.1+2
C.1+2+3 D.1+2+3+4
D

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案