题目内容
8.求函数f(x)=($\frac{1}{2}$)${\;}^{{x}^{2}-2x}$的值域.分析 利用指数函数的性质进行求解即可.
解答 解:设t=x2-2x=(x-1)2-1,
则t≥-1,
则y=($\frac{1}{2}$)t∈(0,2],
故函数的值域为(0,2]
点评 本题主要考查函数值域的计算,利用换元法结合一元二次函数和指数函数的单调性的性质是解决本题的关键.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
13.已知异面直线a与b所成的角为θ;向量$\overrightarrow{m}$和$\overrightarrow{n}$所在直线分别平行于a和b,则恒有( )
| A. | cosθ=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}$ | B. | cos(π-θ)=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}$ | C. | |cosθ|=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}$ | D. | cosθ=$\frac{|\overrightarrow{m}•\overrightarrow{n}|}{|\overrightarrow{m}||\overrightarrow{n}|}$ |
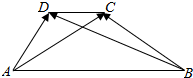 如图,梯形ABCD中,AB∥CD,AB=3CD.
如图,梯形ABCD中,AB∥CD,AB=3CD.