题目内容
20.已知点A(5,0),抛物线C:y2=8x的焦点为F,点P在抛物线C上,若点F恰好在PA的垂直平分线上,则PA的长度为2$\sqrt{6}$.分析 利用已知条件,判断三角形PFA的形状,利用抛物线的性质与抛物线方程求出P的坐标,通过两点间距离公式求解即可.
解答 解:点A(5,0)在x轴上,抛物线C:y2=8x的焦点为F(2,0),
点P在抛物线C上,若点F恰好在PA的垂直平分线上,
可知三角形PFA是等腰三角形,即:|PF|=|AF|,可得|PF|=3,
由抛物线的定义可知,丨PF丨=x+$\frac{p}{2}$=3,则x=1,当x=1时,y=2$\sqrt{2}$,
∴P(1,2$\sqrt{2}$).
则丨PA丨=$\sqrt{(1-5)^{2}+(2\sqrt{2})^{2}}$=2$\sqrt{6}$.
故答案为:2$\sqrt{6}$.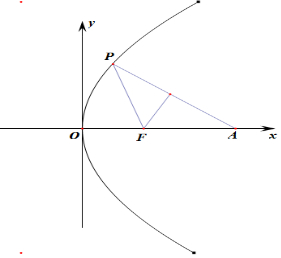
点评 本题考查直线与抛物线的位置关系的应用,抛物线的简单性质的应用,考查计算能力,属于中档题.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
10.函数f(x)=2sin2(2x+$\frac{π}{6}$)-sin(4x+$\frac{π}{3}$)图象的一个对称中心可以为( )
| A. | (-$\frac{5π}{48}$,0) | B. | (-$\frac{7π}{48}$,0) | C. | (-$\frac{5π}{48}$,1) | D. | (-$\frac{7π}{48}$,1) |
15.已知复数z=m+2i,且(1+i)•z是纯虚数,则实数m=( )
| A. | 1 | B. | 2 | C. | -1 | D. | -2 |