题目内容

15．已知复数z=m+2i，且（1+i）•z是纯虚数，则实数m=（　　）
A．1B．2C．-1D．-2

分析 把z代入（1+i）•z，整理后由实部为0且虚部不为0求得m值．

解答 解：∵z=m+2i，
∴（1+i）•z=（1+i）（m+2i）=m-2+（m+2）i，
由（1+i）•z是纯虚数，得m=2．
故选：B．

点评 本题考查复数代数形式的乘除运算，考查复数的基本概念，是基础题．

练习册系列答案
相关题目
5．已知等差数列{an}满足a1=2，a3=8，则数列{an}的公差为（　　）
A．1B．2C．3D．4
6．把2名新生分到甲、乙、丙、丁四个班，甲班必须且只能分配1名新生，则不同的分配方法有（　　）
A．3种B．4种C．6种D．8种
3．已知圆心在x轴上的圆C与直线l：4x+3y-6=0切于点M（$\frac{3}{5}$，$\frac{6}{5}$）．
（1）求圆C的标准方程；
（2）已知N（2，1），经过原点，且斜率为正数的直线L与圆C交于P（x1，y1），Q（x2，y2）两点．
（ⅰ）求证：$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$为定值；
（ii）求|PN|2+|QN|2的最大值．
10．在等差数列{an}中，a15+a16+a17=-45，a9=-36，Sn为其前n项和．
（1）求Sn的最小值，并求出相应的n值；
（2）求Tn=|a1|+|a2|+…+|an|．
20．已知点A（5，0），抛物线C：y2=8x的焦点为F，点P在抛物线C上，若点F恰好在PA的垂直平分线上，则PA的长度为2$\sqrt{6}$．
7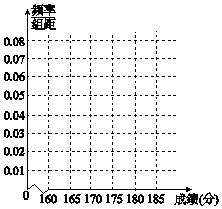．近期中央电视台播出的《中国诗词大会》火遍全国，下面是组委会在选拔赛时随机抽取的100名选手的成绩，按成绩分组，得到的频率分布表如下表示．
组号分组频数频率
第1组[160，165） 0.100
第2组[165，170）① 
第3组[170，175）20②
第4组[175，180）200.200
第5组[180，185）100.100
合计 1001.00
（1）请先求出频率分布表中①、②位置相应的数据，再完成频率分布直方图（用阴影表示）；
（2）为了能选拔出最优秀的选手，组委会决定在笔试成绩高的第3、4、5组中用分层抽样抽取5名学生进入第二轮面试，求第3、4、5组每组各抽取多少名选手进入第二轮面试；
（3）在（2）的前提下，组委会决定在5名选手中随机抽取2名选手接受A考官进行面试，求：第4组至少有一名选手被考官A面试的概率．
4．求下列各式的值：
（1）$\frac{1}{2}$log24+lg20+lg5．
（2）（$\frac{4}{9}$）${\;}^{-\frac{1}{2}}$+（lg3）0-（$\frac{27}{8}$）${\;}^{\frac{2}{3}}$+eln2（其中e=2.71828…）
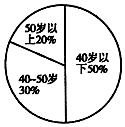17．200名职工年龄分布如图所示，从中随机抽取40名职工作样本，采用系统抽样方式，按1～200编号分为40组，分别为1～5，6～10，…，196～200，第5组抽取号码为23，第9组抽取号码为43；若采用分层抽样，40-50岁年龄段应抽取12人．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网