题目内容
在△ABC中,A=45°,C=105°,a=5,则b= .
考点:正弦定理
专题:解三角形
分析:由A与C的度数求出B的度数,得到sinB的值,再由sinA,a的值,利用正弦定理求出b的值即可.
解答:
解:∵在△ABC中,A=45°,C=105°,a=5,
∴B=30°,
由正弦定理
=
得:b=
=
=
,
故答案为:
∴B=30°,
由正弦定理
| a |
| sinA |
| b |
| sinB |
| asinB |
| sinA |
5×
| ||||
|
5
| ||
| 2 |
故答案为:
5
| ||
| 2 |
点评:此题考查了正弦定理,以及特殊角的三角函数值,熟练掌握正弦定理是解本题的关键.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案
相关题目
已知函数y=sin(x-
),x∈[0,2π],则该函数的单调增区间为( )
| π |
| 3 |
A、[0,
| ||||
B、[
| ||||
C、[
| ||||
D、[0,
|
己知函数f(x)=tx,g(x)=(2-t)x2-4x+l.若对于任一实数x0,函数值f(x0)与g(x0)中至少有一个为正数,则实数t的取值范围是( )
| A、(-∞,-2)∪(0,2] |
| B、(-2,0)∪(-2,2] |
| C、(-2,2] |
| D、(0,+∞) |
在?ABCD中,AC=
,BD=
,周长为18,则这个平行四边形的面积为( )
| 65 |
| 17 |
| A、16 | ||
B、17
| ||
| C、18 | ||
| D、32 |
已知tanα=-
,则sin2α=( )
| 3 |
| 5 |
A、
| ||
B、-
| ||
C、-
| ||
D、
|
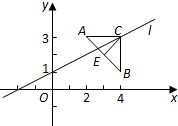 如图,已知点A(2,3),B(4,1),△ABC是以AB为底边的等腰三角形,点C在直线l:x-2y+2=0上.
如图,已知点A(2,3),B(4,1),△ABC是以AB为底边的等腰三角形,点C在直线l:x-2y+2=0上.