题目内容
14．若直线Ax+By+C=0左上方的点（x0，y0）满足Ax0+By0+C＞0，则A•B的符号为负．分析 判断出斜率的正负，从而求出AB的符号即可．
解答 解：首先，只有斜率为正的直线才谈得上左上方和右下方（斜率为负的直线则有左下方和右上方），
斜率为-$\frac{A}{B}$，所以A，B异号，
故答案为：负．
点评 本题考查二无一次不等式的几何意义，解题时要注意特殊值法的合理运用．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
2．设x，y∈[$\frac{1}{3}$，1]，则y+$\frac{x}{\sqrt{4{x}^{2}（{y}^{2}+1）-4x+1}}$的最大值为（ ）
| A． | $\frac{1}{2}$ | B． | 1 | C． | $\frac{3}{2}$ | D． | $\frac{11}{6}$ |
9．
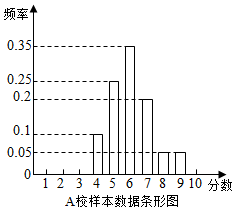某市组织高一全体学生参加计算机操作比赛，等级分为1至10分，随机调阅了A、B两所学校各60名学生的成绩，得到样本数据如表：
B校样本数据统计表
（Ⅰ）计算两校样本数据的均值和方差，并根据所得数据进行比较．
（Ⅱ） 记事件C为“A校学生计算机优秀成绩高于B校学生计算机优秀成绩”．假设7分或7分以上为优秀成绩，两校学生计算机成绩相互独立．根据所给样本数据，以事件发生的频率作为相应事件发生的概率，求C的概率．
某市组织高一全体学生参加计算机操作比赛，等级分为1至10分，随机调阅了A、B两所学校各60名学生的成绩，得到样本数据如表：B校样本数据统计表
| 成绩（分） | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 人数（个） | 0 | 0 | 0 | 9 | 12 | 21 | 9 | 6 | 3 | 0 |
（Ⅱ） 记事件C为“A校学生计算机优秀成绩高于B校学生计算机优秀成绩”．假设7分或7分以上为优秀成绩，两校学生计算机成绩相互独立．根据所给样本数据，以事件发生的频率作为相应事件发生的概率，求C的概率．