题目内容
20.设x,y∈R,给出四个点A(2x-1,y),B(1,1),C(x2+1,4),D(x2-1,1)(1)若$\overrightarrow{AB}$∥$\overrightarrow{CD}$,把y表示成x的函数y=f(x);
(2)对数列{an},设a1=a2=1,且${4}^{{a}_{n+1}}$=$\frac{2}{3}$f(an)+$\frac{4}{3}$,(n≥2,n∈N*),求$\underset{lim}{n→∞}$an.
分析 (1)求出向量的坐标,再由向量共线的坐标表示,即可得到所求函数的解析式;
(2)由题意化简可得an+1=$\frac{1}{2}$an,(n≥2),再由等比数列的通项公式,可得an,再由数列极限的运算性质可得结论.
解答 解:(1)由题意可得$\overrightarrow{AB}$=(2-2x,1-y),$\overrightarrow{CD}$=(-2,-3),
由若$\overrightarrow{AB}$∥$\overrightarrow{CD}$,可得-3(2-2x)=-2(1-y),
即有y=f(x)=3•2x-1-2;
(2)${4}^{{a}_{n+1}}$=$\frac{2}{3}$f(an)+$\frac{4}{3}$,可得
${4}^{{a}_{n+1}}$=$\frac{2}{3}$(3•${2}^{{a}_{n}-1}$-2)+$\frac{4}{3}$=${2}^{{a}_{n}}$,
即有an+1=$\frac{1}{2}$an,(n≥2),
a3=$\frac{1}{2}$a2=$\frac{1}{2}$,
即有an=$\left\{\begin{array}{l}{1,n=1}\\{(\frac{1}{2})^{n-2},n≥2}\end{array}\right.$,
则$\underset{lim}{n→∞}$an=$\underset{lim}{n→∞}$($\frac{1}{2}$)n-2=0.
点评 本题考查等比数列的通项公式的运用,数列极限的求法,同时考查向量的共线的坐标表示,考查运算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.直线y=k(x-3)与双曲线$\frac{x^2}{9}-\frac{y^2}{4}=1$只有一个公共点,则k的值有( )
| A. | 3个 | B. | 2个 | C. | 1个 | D. | 无数个 |
15.若s,t均为正数,且s+t=1,则$\frac{st}{(st+1)(st+4)}$的最大值是( )
| A. | $\frac{4}{85}$ | B. | $\frac{7}{72}$ | C. | $\frac{1}{9}$ | D. | $\frac{1}{7}$ |
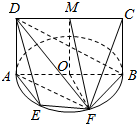 如图所示,矩形ABCD所在的平面垂直圆O所在的平面,AB是圆O的直径,M是CD上一点,且DM=EF,E、F是圆O上的点,∠EAF=∠FAB=30°.
如图所示,矩形ABCD所在的平面垂直圆O所在的平面,AB是圆O的直径,M是CD上一点,且DM=EF,E、F是圆O上的点,∠EAF=∠FAB=30°.