题目内容
12．已知2sinα+cosα=0，则sin2α-3cos2α-sin2α=（ ）| A． | -$\frac{17}{5}$ | B． | -$\frac{17}{4}$ | C． | -$\frac{16}{5}$ | D． | -2 |
分析 由条件利用同角三角函数的基本关系求得tanα的值，可得sin2α-3cos2α-sin2α的值．
解答 解：∵已知2sinα+cosα=0，∴tanα=-$\frac{1}{2}$，
则sin2α-3cos2α-sin2α=$\frac{2sinαcosα-{3cos}^{2}α{-sin}^{2}α}{{sin}^{2}α{+cos}^{2}α}$
=$\frac{2tanα-3{-tan}^{2}α}{{tan}^{2}α+1}$=$\frac{-1-3-\frac{1}{4}}{\frac{1}{4}+1}$=-$\frac{17}{5}$，
故选：A．
点评 本题主要考查同角三角函数的基本关系，属于基础题．
练习册系列答案
七彩题卡口算应用一点通系列答案
相关题目
2．已知lg5=m，lg7=n，则log27=（ ）
| A． | $\frac{m}{n}$ | B． | $\frac{n}{1-m}$ | C． | $\frac{1-n}{m}$ | D． | $\frac{1+n}{1+m}$ |
3．函数y=x|lnx|的图象大致为（ ）
| A． |  | B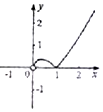． |  | C． |  | D． |  |
20．不等式|2x+3|＜1的解集为（ ）
| A． | （-2，-1） | B． | （-∞，-2）∪（-1，+∞） | C． | （1，2） | D． | （-∞，1）∪（2，+∞） |
4．已知直线：bx+ay=0与直线：x-2y+2=0垂直，则二次函数f（x）=ax2-bx+a的说法正确的是（ ）
| A． | f（x）开口方向朝上 | B． | f（x）的对称轴为x=1 | C． | f（x）在（-∞，-1）上递增 | D． | f（x）在（-∞，-1）上递减 |
1．已知P为抛物线y2=4x上的动点，直线l1：x=-1，直线l2：x+y+3=0，则P点到直线l1，l2距离之和的最小值为（ ）
| A． | 2$\sqrt{2}$ | B． | 4 | C． | $\sqrt{2}$ | D． | $\frac{3}{2}$$\sqrt{2}$ |