题目内容
15.化简:sin2αtanα+$\frac{co{s}^{2}α}{tanα}$+2sinαcosα-$\frac{1-cosα}{sinαcosα}$.分析 由条件利用同角三角函数的基本关系,完全平方公式化简所给的式子,可得结果.
解答 解:sin2αtanα+$\frac{co{s}^{2}α}{tanα}$+2sinαcosα-$\frac{1-cosα}{sinαcosα}$=$\frac{{sin}^{3}α}{cosα}$+$\frac{{cos}^{3}α}{sinα}$+2sinαcosα-$\frac{1-cosα}{sinαcosα}$
=$\frac{{sin}^{4}α{+cos}^{4}α+{2sin}^{2}{αcos}^{2}α}{sinαcosα}$-$\frac{1-cosα}{sinαcosα}$=$\frac{{{(sin}^{2}α{+cos}^{2}α)}^{2}}{sinαcosα}$-$\frac{1-cosα}{sinαcosα}$
=$\frac{1}{sinαcosα}$-$\frac{1-cosα}{sinαcosα}$=$\frac{1}{sinα}$.
点评 本题主要考查三角函数的化简求值,属于基础题.

练习册系列答案
相关题目
3.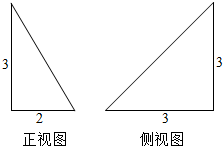 已知一个三棱锥的正视图,侧视图均为直角三角形,其形状及尺寸如图,则该三棱锥的俯视图的面积为( )
已知一个三棱锥的正视图,侧视图均为直角三角形,其形状及尺寸如图,则该三棱锥的俯视图的面积为( )
 已知一个三棱锥的正视图,侧视图均为直角三角形,其形状及尺寸如图,则该三棱锥的俯视图的面积为( )
已知一个三棱锥的正视图,侧视图均为直角三角形,其形状及尺寸如图,则该三棱锥的俯视图的面积为( )| A. | 3 | B. | 6 | C. | $\frac{9}{2}$或9 | D. | 3或6 |