题目内容
7.已知椭圆方程C为:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1.(a>b>0)椭圆的右焦点为(1,0),离心率为e=$\frac{1}{2}$,直线l:y=kx+m与椭圆C相交于A、B两点,且KOAKOB=-$\frac{3}{4}$.(I)求椭圆的C的方程;
(Ⅱ)求△AOB的面积.
分析 (Ⅰ)由题意求出c,结合离心率求得a,再由隐含条件求得b,则椭圆方程可求;
(Ⅱ)联立直线方程和椭圆方程,设出A,B的坐标,利用根与系数的关系求出A,B的横纵坐标的乘积,再由kOAkOB=-$\frac{3}{4}$得到k与m的关系,利用弦长公式求得弦长,由点到直线的距离公式求出坐标原点O到直线l的距离,代入三角形面积公式得答案.
解答 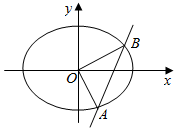 解:(Ⅰ)由题意可得,c=1,$e=\frac{c}{a}=\frac{1}{2}$,则a=2,
解:(Ⅰ)由题意可得,c=1,$e=\frac{c}{a}=\frac{1}{2}$,则a=2,
∴b2=a2-c2=3,
则椭圆方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$;
(Ⅱ)如图,联立$\left\{\begin{array}{l}{y=kx+m}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$,得(3+4k2)x2+8kmx+4m2-12=0.
△=64k2m2-4(3+4k2)(4m2-12)=48(4k2-m2+3),
设A(x1,y1),B(x2,y2),
则${x}_{1}+{x}_{2}=-\frac{8km}{3+4{k}^{2}}$,${x}_{1}{x}_{2}=\frac{4{m}^{2}-12}{3+4{k}^{2}}$,
∵kOAkOB=-$\frac{3}{4}$,
∴$\frac{{y}_{1}{y}_{2}}{{x}_{1}{x}_{2}}=\frac{{k}^{2}{x}_{1}{x}_{2}+km({x}_{1}+{x}_{2})+{m}^{2}}{{x}_{1}{x}_{2}}$=$\frac{{k}^{2}•\frac{4{m}^{2}-12}{3+4{k}^{2}}-\frac{8{k}^{2}{m}^{2}}{3+4{k}^{2}}+{m}^{2}}{\frac{4{m}^{2}-12}{3+4{k}^{2}}}=-\frac{3}{4}$,
整理得:$\frac{3{m}^{2}-12{k}^{2}}{4{m}^{2}-12}=-\frac{3}{4}$,即2m2=4k2+3.
|AB|=$\sqrt{1+{k}^{2}}•\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{1+{k}^{2}}\sqrt{\frac{64{k}^{2}{m}^{2}}{(3+4{k}^{2})^{2}}-\frac{16{m}^{2}-48}{3+4{k}^{2}}}$
=$2\sqrt{6}\sqrt{1+{k}^{2}}\sqrt{\frac{4{k}^{2}+3}{(3+4{k}^{2})^{2}}}$.
原点O到直线kx-y+m=0的距离d=$\frac{|m|}{\sqrt{{k}^{2}+1}}$,
∴△AOB的面积S=$\frac{1}{2}|AB|d=\frac{1}{2}×2\sqrt{6}\sqrt{1+{k}^{2}}\sqrt{\frac{4{k}^{2}+3}{(3+4{k}^{2})^{2}}}•\frac{|m|}{\sqrt{{k}^{2}+1}}$
=$\sqrt{3}•\frac{3+4{k}^{2}}{3+4{k}^{2}}=\sqrt{3}$.
点评 本题考查椭圆方程的求法,考查了直线和椭圆位置关系的应用,训练了弦长公式及点到直线的距离公式的应用,是中档题.

 天天向上口算本系列答案
天天向上口算本系列答案157 161 170 180 181 172 162 157 191 182 181 173 174 165 158

164 159 159 168 169 176 178 158 169 176 187 184 175 169 175
(1)完成频数分布表,并作出频率分布直方图.
| 挂果个数区间 | [155,165) | [165,175) | [175,185) | [185,195] |
| 频数 |