题目内容
7.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$|=1,|$\overrightarrow{b}$|=2,$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为120°.(1)求$\overrightarrow{a}$•$\overrightarrow{b}$及|$\overrightarrow{a}$+$\overrightarrow{b}$|;
(2)设向量$\overrightarrow{a}$+$\overrightarrow{b}$与$\overrightarrow{a}$-$\overrightarrow{b}$的夹角为θ,求cosθ的值.
分析 (1)根据数量积的计算公式即可求出$\overrightarrow{a}•\overrightarrow{b}$,而由$|\overrightarrow{a}+\overrightarrow{b}{|}^{2}=(\overrightarrow{a}+\overrightarrow{b})^{2}$即可求出$|\overrightarrow{a}+\overrightarrow{b}|$;
(2)同理可以求出$|\overrightarrow{a}-\overrightarrow{b}|$的值,而可求出$(\overrightarrow{a}+\overrightarrow{b})•(\overrightarrow{a}-\overrightarrow{b})={\overrightarrow{a}}^{2}-{\overrightarrow{b}}^{2}=-3$,从而根据向量夹角余弦的计算公式即可求出cosθ.
解答 解:(1)$\overrightarrow{a}•\overrightarrow{b}=|\overrightarrow{a}||\overrightarrow{b}|cos120°$=$1×2×(-\frac{1}{2})=-1$;
∴$|\overrightarrow{a}+\overrightarrow{b}{|}^{2}=(\overrightarrow{a}+\overrightarrow{b})^{2}$=${\overrightarrow{a}}^{2}+2\overrightarrow{a}•\overrightarrow{b}+{\overrightarrow{b}}^{2}={1}^{2}+2×(-1)+{2}^{2}=3$;
∴$|\overrightarrow{a}+\overrightarrow{b}|=\sqrt{3}$;
(2)同理可求得$|\overrightarrow{a}-\overrightarrow{b}|=\sqrt{7}$;
$(\overrightarrow{a}+\overrightarrow{b})•(\overrightarrow{a}-\overrightarrow{b})={\overrightarrow{a}}^{2}-{\overrightarrow{b}}^{2}={1}^{2}-{2}^{2}=-3$;
∴$cosθ=\frac{(\overrightarrow{a}+\overrightarrow{b})•(\overrightarrow{a}-\overrightarrow{b})}{|\overrightarrow{a}+\overrightarrow{b}||\overrightarrow{a}-\overrightarrow{b}|}=\frac{-3}{\sqrt{3}•\sqrt{7}}$=$-\frac{\sqrt{21}}{7}$.
点评 考查向量数量积的运算及其计算公式,根据$|\overrightarrow{a}+\overrightarrow{b}{|}^{2}=(\overrightarrow{a}+\overrightarrow{b})^{2}$求$|\overrightarrow{a}+\overrightarrow{b}|$的方法,以及向量夹角余弦的计算公式.

| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $-\frac{1}{3}$ | D. | $-\frac{1}{2}$ |
157 161 170 180 181 172 162 157 191 182 181 173 174 165 158

164 159 159 168 169 176 178 158 169 176 187 184 175 169 175
(1)完成频数分布表,并作出频率分布直方图.
| 挂果个数区间 | [155,165) | [165,175) | [175,185) | [185,195] |
| 频数 |
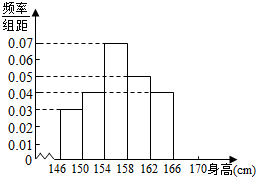 为了了解某校高一女生的身高情况,随机抽取M个高一女生测量身高,所得数据整理后列出频率分布如表:
为了了解某校高一女生的身高情况,随机抽取M个高一女生测量身高,所得数据整理后列出频率分布如表:| 组 别 | 频数 | 频率 |
| [146,150) | 6 | 0.12 |
| [150,154) | 8 | 0.16 |
| [154,158) | 14 | 0.28 |
| [158,162) | 10 | 0.20 |
| [162,166) | 8 | 0.16 |
| [166,170) | m | n |
| 合 计 | M | 1 |
(Ⅱ)在图中补全频率分布直方图;
(Ⅲ)根据频率分布直方图估计该校高一女生身高的中位数(保留两位小数)

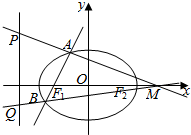 如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左焦点为F1(-1,0),离心率是e,点(1,e)在椭圆上.
如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左焦点为F1(-1,0),离心率是e,点(1,e)在椭圆上.