题目内容
10.△ABC的两个顶点为A(-1,0),B(1,0),△ABC周长为6,则C点轨迹为以A,B为焦点的椭圆(除去椭圆与x轴的交点),方程为$\frac{x^2}{4}+\frac{y^2}{3}=1({y≠0})$.分析 根据三角形的周长和定点,得到点A到两个定点的距离之和等于定值,得到点C的轨迹是椭圆,椭圆的焦点在x轴上,写出椭圆的方程,去掉不合题意的点.
解答 解:∵△ABC的两顶点A(-1,0),B(1,0),△ABC周长为6,
∴AB=2,BC+AC=4,
∵4>2,∴点C到两个定点的距离之和等于定值,点C满足椭圆的定义,
∴点C的轨迹是以A,B为焦点的椭圆(除去椭圆与x轴的交点),
∴2a=4,2c=2,∴a=2,c=1,b=$\sqrt{3}$,
∴椭圆的标准方程是$\frac{x^2}{4}+\frac{y^2}{3}=1({y≠0})$,
故答案为以A,B为焦点的椭圆(除去椭圆与x轴的交点),方程为$\frac{x^2}{4}+\frac{y^2}{3}=1({y≠0})$.
点评 本题考查轨迹方程的求法,注意椭圆的定义的应用是关键.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
17.某单位要在800名员工中抽去80名员工调查职工身体健康状况,其中青年员工400名,中年员工300名,老年员工100名,下列说法错误的是( )
| A. | 老年人应作为重点调查对象,故抽取的老年人应超过40名 | |
| B. | 每个人被抽到的概率相同为$\frac{1}{10}$ | |
| C. | 应使用分层抽样抽取样本调查 | |
| D. | 抽出的样本能在一定程度上反映总体的健康状况 |
18.有各不相同的5红球、3黄球、2白球,事件A:从红球和黄球中各选1球,事件B:从所有球中选取2球,则事件A发生是事件B发生的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
15.在△ABC的三边分别为a,b,c,a2=b2+c2-bc,则A等于( )
| A. | 30° | B. | 60° | C. | 75° | D. | 120° |
2.若变量x,y满足约束条件$\left\{\begin{array}{l}y≥x\\ x+y≤2\\ x≥a.\end{array}\right.$且目标函数z=2x-y的最大值是最小值的2倍,则a的值是( )
| A. | $\frac{1}{2}$ | B. | 4 | C. | 3 | D. | $\frac{4}{5}$ |
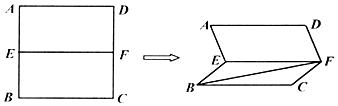 如图,已知E,F分别是正方形ABCD的边AB、CD的中点,现将正方形沿EF折成60°的二面角,则异面角直线AE与BF所成角的余弦值是$\frac{\sqrt{5}}{10}$.
如图,已知E,F分别是正方形ABCD的边AB、CD的中点,现将正方形沿EF折成60°的二面角,则异面角直线AE与BF所成角的余弦值是$\frac{\sqrt{5}}{10}$.