题目内容
已知函数![]() 为实常数).
为实常数).
(I)当![]() 时,求函数
时,求函数![]() 在
在![]() 上的最小值;
上的最小值;
(Ⅱ)若方程![]() (其中
(其中![]() )在区间
)在区间![]() 上有解,求实数
上有解,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)证明:![]() (参考数据:
(参考数据:![]() )
)
解:(Ⅰ)当![]() 时,
时,![]() ,
,![]() ,令
,令![]() ,又
,又![]() ,
,
![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.![]() 当
当![]() 时,
时,![]() .
.![]() 的最小值为
的最小值为![]() . ….4分
. ….4分
(Ⅱ) ![]() 在
在![]() 上有解
上有解![]() 在
在![]() 上有解
上有解![]() 在
在![]() 上有解.令
上有解.令![]() ,
,
![]() ,
,
令![]() ,又
,又![]() ,解得:
,解得:![]() .
.
![]() 在
在![]() 上单调递增,
上单调递增,![]() 上单调递减,
上单调递减,
又![]() .
.![]() .即
.即![]() .故
.故![]() .……9分
.……9分
(Ⅲ)设![]() ,
,![]()
由(I),![]() ,
,![]() .
.![]() .
.
![]()
![]() .
.
![]()
![]() .
.
构造函数![]() ,
,![]() 当
当![]() 时,
时,![]() .
.
![]() 在
在![]() 上单调递减,即
上单调递减,即![]() .
.![]() 当
当![]() 时,
时,![]() .
.
![]() .即
.即![]() .
.
![]() .
.
故![]() . …14分
. …14分

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
 为实常数).
为实常数). 时,求函数
时,求函数 在
在 上的最小值;
上的最小值; (其中
(其中 )在区间
)在区间 上有解,求实数
上有解,求实数 的取值范围;
的取值范围;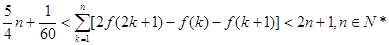 (参考数据:
(参考数据: )
)