题目内容
7.下列命题中,正确的是( )| A. | θ=$\frac{π}{4}$是f(x)=sin(x-2θ)的图象关于y轴对称的充分不必要条件 | |
| B. | |a|-|b|=|a-b|的充要条件是a与b的方向相同 | |
| C. | b=$\sqrt{ac}$是a,b,c三数成等比数列的充分不必要条件 | |
| D. | m=3是直线(m+3)x+my-2=0与mx-6y+5=0互相垂直的充要条件 |
分析 解:A,θ=$\frac{π}{4}$时,f(x)=sin(x-2θ)=-cosx是偶函数,其图象关于y轴对称,若f(x)=sin(x-2θ)的图象关于y轴对称⇒-2θ=kπ+$\frac{π}{2}$;
B,向量$\overrightarrow{a}=\overrightarrow{0}$时,|a|-|b|=|a-b|成立;
C,b=0时,a,b,c三数不成等比数列;
D,直线(m+3)x+my-2=0与mx-6y+5=0互相垂直时,m=3或0.
解答 解:对于A,θ=$\frac{π}{4}$时,f(x)=sin(x-2θ)=-cosx是偶函数,其图象关于y轴对称,若f(x)=sin(x-2θ)的图象关于y轴对称⇒-2θ=kπ+$\frac{π}{2}$,故正确;
对于B,向量$\overrightarrow{a}=\overrightarrow{0}$时,|a|-|b|=|a-b|成立,故错;
对于C,b=0时,a,b,c三数不成等比数列,故错;
对于D,直线(m+3)x+my-2=0与mx-6y+5=0互相垂直时,m=3或0,故错.
故选:A.
点评 本题考查了命题真假的判定,涉及到很多基础知识,属于基础题.

练习册系列答案
相关题目
17.设E,F分别为平行四边形ABCD中AB,AD的中点,$\overrightarrow{EC}$+$\overrightarrow{FC}$=( )
| A. | $\frac{1}{2}$$\overrightarrow{AC}$ | B. | $\overrightarrow{AC}$ | C. | $\frac{3}{2}$$\overrightarrow{AC}$ | D. | 2$\overrightarrow{AC}$ |
15.△ABC的内角A,B满足cosAcosB>sinAsinB,则△ABC是( )
| A. | 锐角三角形 | B. | 钝角三角形 | C. | 直角三角形 | D. | 等边三角形 |
19.函数y=ax,x∈[-1,2]的最大值与函数f(x)=x2-2x+3的最值相等,则a的值为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{2}$或2 | C. | $\frac{1}{2}$或2 | D. | $\frac{1}{2}或\sqrt{2}$ |
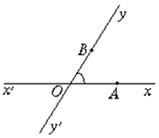 如图,有两条相交成60°角的直线xx′,yy′,交点是O,甲、乙分别在Ox,Oy上,起初甲离O点3km,乙离O点1km,后来两人同时用每小时4km的速度,甲沿xx′方向,乙沿y′y方向步行,问:
如图,有两条相交成60°角的直线xx′,yy′,交点是O,甲、乙分别在Ox,Oy上,起初甲离O点3km,乙离O点1km,后来两人同时用每小时4km的速度,甲沿xx′方向,乙沿y′y方向步行,问: