题目内容

2．设函数f（x）=lg（2x-3）的定义域为集合M，函数g（x）=$\frac{\sqrt{x-3}}{\sqrt{x-1}}$的定义域为集合N．求：
（1）集合M，N；
（2）集合M∪N，∁RN．

分析 （1）对数的真数大于0求出集合M；开偶次方的被开方数非负且分母不等于0，求出集合N；
（2）直接利用集合的运算求出集合M∪N，CRN．

解答 解：（1）由题意2x-3＞0 故{x|x＞$\frac{3}{2}$}；
因为$\left\{\begin{array}{l}{x-3≥0}\\{x-1＞0}\end{array}\right.$，故N={x|x≥3}
（2）由（1）可知M∪N={x|x＞$\frac{3}{2}$}，∁RN={x|x＜3}

点评 本题考查对数函数的定义域，交集、并集、补集及其运算；是基础题．

练习册系列答案
相关题目
12．已知函数f（x）=a3x+1，g（x）=（$\frac{1}{a}$）5x-2，其中a＞0，且a≠1．
（1）若0＜a＜1，求满足f（x）＜1的x的取值范围；
（2）求关于x的不等式f（x）≥g（x）的解集．
13．（用“＞”或“＜”填空）若a＞b，则a-4＞b-4；
（用命题的真值1或0填空）设p：若a，b都是奇数，则a+b是奇数，p=0．
10．命题“?x0∈R，asinx0+cosx0≥2”为假命题，则实数a的取值范围是（-$\sqrt{3}$，$\sqrt{3}$）．
17．在△ABC中，若2sin$\frac{B}{2}$•cos$\frac{B}{2}$•sinC=cos2$\frac{A}{2}$，则△ABC是（　　）
A．等边三角形B．等腰三角形C．非等腰三角形D．直角三角形
7．下列命题中，正确的是（　　）
A．θ=$\frac{π}{4}$是f（x）=sin（x-2θ）的图象关于y轴对称的充分不必要条件
B．|a|-|b|=|a-b|的充要条件是a与b的方向相同
C．b=$\sqrt{ac}$是a，b，c三数成等比数列的充分不必要条件
D．m=3是直线（m+3）x+my-2=0与mx-6y+5=0互相垂直的充要条件
14．已知集合A={ x|-2＜x＜6}，B={ x|4＜x＜7}，则A∩B=（　　）
A．{4，5，6}B．{5}C．（-2，7）D．（4，6）
11．已知圆N经过点A（3，1），B（-1，3），且它的圆心在直线3x-y-2=0上．
（Ⅰ）求圆N的方程；
（Ⅱ）求圆N关于直线x-y+3=0对称的圆的方程．
（Ⅲ）若点D为圆N上任意一点，且点C（3，0），求线段CD的中点M的轨迹方程．
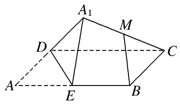12．如图，矩形ABCD中，E为边AB的中点，将△ADE沿直线DE翻转成△A1DE．若M为线段A1C的中点，则在△ADE翻转过程中，下列说法正确的是①②．（填序号）
①MB∥平面A1DE；
②|BM|是定值；
③A1C⊥DE．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网