题目内容
16.设$\sqrt{2}a+$1,a,a-1为钝角三角形的三边,则a的取值范围为(2+$\sqrt{2}$,+∞).分析 由题意推出三角形的最大边,列出满足钝角三角形的关系式 $\left\{\begin{array}{l}{a+a-1>\sqrt{2}a+1}\\{{a}^{2}+(a-1)^{2}<(\sqrt{2}a+1)^{2}}\end{array}\right.$,解出a的范围即可.
解答 解:∵钝角三角形的三边$\sqrt{2}a+$1,a,a-1,$\sqrt{2}a+$1为最大边,
则满足$\left\{\begin{array}{l}{a+a-1>\sqrt{2}a+1}\\{{a}^{2}+(a-1)^{2}<(\sqrt{2}a+1)^{2}}\end{array}\right.$,解得:a>$\frac{2}{2-\sqrt{2}}$=2+$\sqrt{2}$,
故答案为:(2+$\sqrt{2}$,+∞).
点评 此题考查了余弦定理,三角形的边角关系,以及不等式的解法,关键是掌握三角形任意两边之和大于第三边,属于中档题.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
13.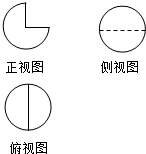 某几何体的三视图如图所示,其中俯视图与侧视图是半径均为$\sqrt{2}$的圆,则该几何体的表面积是( )
某几何体的三视图如图所示,其中俯视图与侧视图是半径均为$\sqrt{2}$的圆,则该几何体的表面积是( )
 某几何体的三视图如图所示,其中俯视图与侧视图是半径均为$\sqrt{2}$的圆,则该几何体的表面积是( )
某几何体的三视图如图所示,其中俯视图与侧视图是半径均为$\sqrt{2}$的圆,则该几何体的表面积是( )| A. | 14π | B. | 12π | C. | 10π | D. | 8π |