题目内容
7.求函数y=$\frac{1}{x}$过点(2,0)的切线方程.分析 求过点的切线方程一般采取先设切点坐标,然后进行求解.本题先设出切点坐标,然后求出切线方程,将点P的坐标代入即可求出切点坐标,最后利用代入法求出切线方程即可.
解答 解:设切点坐标为(x0,$\frac{1}{{x}_{0}}$)
由于y'|x=x0=-$\frac{1}{{{x}_{0}}^{2}}$,故切线方程为y-$\frac{1}{{x}_{0}}$=-$\frac{1}{{{x}_{0}}^{2}}$(x-x0),
∵y=$\frac{1}{x}$过点(2,0),
∴0-$\frac{1}{{x}_{0}}$=-$\frac{1}{{{x}_{0}}^{2}}$(2-x0),
解得x0=1,
故切点坐标为(1,1),
∴切线方程为:y-1=-(x-1),
即为x+y-2=0.
点评 本题主要考查了利用导数研究曲线上某点切线方程,考查运算求解能力、推理能力,属于基础题.

练习册系列答案
相关题目
17.已知集合A={-1,1},B={x|x∈R,1≤2x≤4},则A∩B等于( )
| A. | {0,1} | B. | {-1,1} | C. | {1} | D. | {-1,0,1} |
12.某商店每天以每瓶5元的价格从奶厂购进若干瓶24小时新鲜牛奶,然后以每瓶8元的价格出售,如果当天该牛奶卖不完,则剩下的牛奶就不再出售,由奶厂以每瓶2元的价格回收处理.
(1)若商场一天购进20瓶牛奶,求当天的利润y(单位:元)关于当天需求量n(单位:瓶,n∈N)的函数解析式;(2)商店记录了50天该牛奶的日需求量(单位:瓶),整理得下表:
假设商店一天购进20瓶牛奶,以50天记录的各需求量的频率作为各需求量发生概率,求当天利润低于60元的概率.
(1)若商场一天购进20瓶牛奶,求当天的利润y(单位:元)关于当天需求量n(单位:瓶,n∈N)的函数解析式;(2)商店记录了50天该牛奶的日需求量(单位:瓶),整理得下表:
| 日需求量n(瓶) | 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| 频数 | 5 | 5 | 8 | 12 | 10 | 6 | 4 |
4.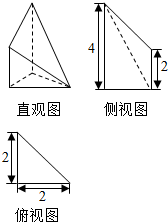 高为4的直三棱柱被削去一部分后得到一个几何体,它的直观图和三视图中的侧视图、俯视图如图所示,则该几何体的体积是原直三棱柱的体积的( )
高为4的直三棱柱被削去一部分后得到一个几何体,它的直观图和三视图中的侧视图、俯视图如图所示,则该几何体的体积是原直三棱柱的体积的( )
 高为4的直三棱柱被削去一部分后得到一个几何体,它的直观图和三视图中的侧视图、俯视图如图所示,则该几何体的体积是原直三棱柱的体积的( )
高为4的直三棱柱被削去一部分后得到一个几何体,它的直观图和三视图中的侧视图、俯视图如图所示,则该几何体的体积是原直三棱柱的体积的( )| A. | $\frac{3}{4}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{8}$ |
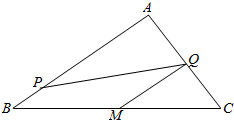 如图,在Rt△ABC中,AB=4,AC=3,∠A=90°,$\overrightarrow{AP}$=m$\overrightarrow{PB}$,$\overrightarrow{AQ}$=n$\overrightarrow{QC}$,m,n>0,且满足$\frac{1}{m}$+$\frac{1}{n}$=$\frac{1}{2}$,M是BC的中点,对任意的λ∈R,|λ•$\overrightarrow{QP}$+$\overrightarrow{QM}$|的最小值记为f(m),则对任意m>0,f(m)的最大值为$\frac{1}{2}$.
如图,在Rt△ABC中,AB=4,AC=3,∠A=90°,$\overrightarrow{AP}$=m$\overrightarrow{PB}$,$\overrightarrow{AQ}$=n$\overrightarrow{QC}$,m,n>0,且满足$\frac{1}{m}$+$\frac{1}{n}$=$\frac{1}{2}$,M是BC的中点,对任意的λ∈R,|λ•$\overrightarrow{QP}$+$\overrightarrow{QM}$|的最小值记为f(m),则对任意m>0,f(m)的最大值为$\frac{1}{2}$.