题目内容

14．设集合M={x|x2-x-2＜0}，N={x|x≤k}，若M∩N=M，则k的取值范围是（　　）
A．（-∞，2]B．[-1，+∞）C．（-1，+∞）D．[2，+∞）

分析 求出集合N中不等式的解集，根据两集合的交集为M，得到M为N的子集，列出关于k的不等式，求出不等式的解集得到k的范围．

解答 解：∵M∩N=M，
∴M⊆N，
∵M={x|-1＜x＜2}，N={x|x≤k}，
∴k≥2．
故选D．

点评 此题常考了交集及其运算，以及集合间的包含关系，其中根据题意得出M是N的子集是解本题的关键．

练习册系列答案
相关题目
4．过抛物线y2=4x的焦点F的直线交该抛物线于A，B两点，若|AF|=3，|BF|=5，则xA+xB=（　　）
A．4B．6C．8D．5
5．已知函数f（x）=ex-ax2，e=2.71828…，曲线y=f（x）在点（1，f（1））处的切线方程为y=（e-2）x+b．
（1）求a，b的值；
（2）设x≥0，求证：f（x）＞x2+4x-14．
2．为推动乒乓球运动的发展，由甲乙两乒乓球协会协商进行友谊赛，现有来自甲协会的运动员4名，其中种子选手2名；乙协会的运动员5名，其中种子选手3名，从这9名运动员中随机选择4人参加比赛．
（Ⅰ）设A为事件“选出的4人中恰有2名种子选手，且这2名种子选手来自同一个协会”，求事件A发生的概率；
（Ⅱ）设X为选出的4人中种子选手的人数，求随机变量X的分布列和数学期望．
9．已知向量$\overrightarrow a，\overrightarrow b$满足$\overrightarrow a=（{1，\sqrt{3}}），|{\overrightarrow b}|=1$，且$\overrightarrow a+λ\overrightarrow b=\overrightarrow 0$，则λ=±2．
19．在等差数列{an}中，已知a1+a2+a3=9，a2a4=21，数列{bn}满足$\frac{b_1}{a_1}+\frac{b_2}{a_2}+…+\frac{b_n}{a_n}=1-\frac{1}{2^n}（{n∈{N^*}}），{S_n}={b_1}+{b_2}+…+{b_n}$，若Sn＞2，则n的最小值为（　　）
A．5B．4C．3D．2
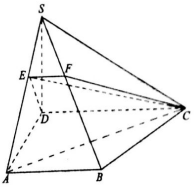6．如图，在直角梯形ABCD中，∠ADC=∠BAD=90°，AB=AD=1，CD=2，平面SAD⊥平面ABCD，平面SDC⊥平面ABCD，SD=$\sqrt{3}$，在线段SA上取一点E（不含端点）使EC=AC，截面CDE交SB于点F．
（1）求证：EF∥CD；
（2）求三棱锥S-DEF的体积．
3．已知集合M={x|lg（x-2）≤0}，N={x|-1≤x≤3}，则M∪N=（　　）
A．{x|x≤3}B．{x|2＜x＜3}C．{x|-1≤x≤3}D．R
4．二项式${（{{x^2}-\frac{1}{x}}）^6}$的展开式中（　　）
A．不含x9项B．含x4项C．含x2项D．不含x项

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网