题目内容
3.数列{an}满足Sn=2n-an(n∈N*).(1)计算a1、a2、a3,并猜想an的通项公式;
(2)用数学归纳法证明(1)中的猜想.
分析 (1)利用递推关系式,通过n=1,2,3求解a1、a2、a3,猜想an的通项公式;
(2)利用数学归纳法的证明步骤,证明猜想即可.
解答 解:(1)当n=1时,a1=S1=2-a1,∴a1=1;
当n=2时,a1+a2=S2=2×2-a2,∴a2=$\frac{3}{2}$;
当n=3时,a1+a2+a3=S3=2×3-a3,∴a3=$\frac{7}{4}$.
由此猜想an=$\frac{{2}^{n}-1}{{2}^{n-1}}$(n∈N*)
(2)证明:①当n=1时,a1=1结论成立,
②假设n=k(k≥1,且k∈N*)时结论成立,
即ak=$\frac{{2}^{k}-1}{{2}^{k-1}}$,
当n=k+1时,ak+1=Sk+1-Sk=2(k+1)-ak+1-2k+ak=2+ak-ak+1,∴2ak+1=2+ak
∴ak+1=$\frac{2+ak}{2}$=$\frac{{2}^{k+1}-1}{{2}^{k}}$,
∴当n=k+1时结论成立,于是对于一切的自然数n∈N*,an=$\frac{{2}^{n}-1}{{2}^{n-1}}$成立
点评 本题考查数列的应用,数学归纳法的证明,考查计算能力.

练习册系列答案
相关题目
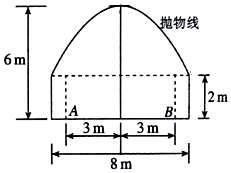 如图所示,一隧道内设双行线公路,其截面由一个长方形和抛物线构成,为保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方向上高度之差至少要有0.5米,已知行车道总宽度|AB|=6米,那么车辆通过隧道的限制高度是多少米?
如图所示,一隧道内设双行线公路,其截面由一个长方形和抛物线构成,为保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方向上高度之差至少要有0.5米,已知行车道总宽度|AB|=6米,那么车辆通过隧道的限制高度是多少米?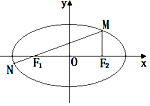 设F1,F2分别是椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左右焦点,M是椭圆C上一点,且直线MF2与x轴垂直,直线MF1与C的另一个交点为N.
设F1,F2分别是椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左右焦点,M是椭圆C上一点,且直线MF2与x轴垂直,直线MF1与C的另一个交点为N.