题目内容
4．已知集合A={x∈Z|y=ln（8x-x2）}，集合M={x||x|＜4，x∈R}，若N=A∩M则N的非空子集的个数为（ ）| A． | 6 | B． | 7 | C． | 8 | D． | 10 |
分析 列举出集合A中的元素，求出A与M的交集确定出集合N，求出N的非空子集即可．
解答 解：∵A={x∈Z|y=ln（8x-x2）}={1，2，3，4，5，6，7}，M={-3，-2，-1，0，1，2，3}，
∴N=A∩M={1，2，3}，
则N的非空子集个为23-1=7．
故选：B．
点评 此题考查了交集及其运算，以及子集，熟练掌握交集的定义是解本题的关键．
练习册系列答案
相关题目
9．已知函数f（x）=sin2x+acos2x（x∈R，a为∈R），若将其图象向右平移$\frac{π}{6}$个单位长度后，所得函数的一个对称中心为（$\frac{π}{2}$，0），则a的值为（ ）
| A． | $\sqrt{3}$ | B． | -1 | C． | 1 | D． | -$\frac{\sqrt{3}}{3}$ |
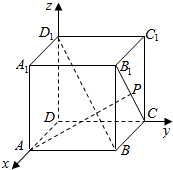如图所示，正方体ABCD-A1B1C1D1的棱长为1，以D为原点，以正方体的三条棱DA，DC，DD1所在的直线分别为x轴，y轴，z轴建立空间直角坐标系，若点P在正方体的侧面BCC1B1及其边界上运动，并且总是保持AP⊥BD1，则下列点P的坐标①（1，1，1），②（0，1，0），③（1，1，0），④（0，1，1），⑤（$\frac{1}{2}$，1，$\frac{1}{2}$）中正确的是①②⑤．