题目内容
如表所示,将数以斜线作如下分群:(1),(2,3),(4,5,6),(8,12,10,7),(16,24,20,14,9),…并顺次称其为第1群,第2群,第3群,第4群,…,
则第n群中n个数的和等于 .
| 1 | 3 | 5 | 7 | 9 | … |
| 2 | 6 | 10 | 14 | 18 | … |
| 4 | 12 | 20 | 28 | 36 | … |
| 8 | 24 | 40 | 56 | 72 | … |
| 16 | 48 | 80 | 112 | 144 | … |
| … | … | … | … | … | … |
考点:归纳推理
专题:推理和证明
分析:观察数列的每一列,得到第一个数列,第2个数列,…都是以2为公比的等比数列,不难求出第6类中的第2项;第n类中n个数表示出后,求出和即可.
解答:
解:由题意数列可以转化为:
1
2 3
4 6 5
8 12 10 7
16 24 20 14 9
32 48 40 28 19 11
…
可知每一列都是等比数列,每一行最后一个数是等差数列,公差为2,
所以第6类中的第2项是:3×24=48.
第n个类中n个数为:Sn=1×2 n-1+3×2n-2+5×2 n-3+…+(2n-1)•2 0…①
2Sn=1×2 n+3×2n-1+5×2 n-2+…+(2n-1)•2 1…②,
②-①得,Sn=2 n+2×2n-1+2×2 n-2+…+2•2 1-2n+1
=2 n+2n+2 n-1+…+2 2-2n+1
=2n+
-2n+1
=3•2n-2n-348,
故答案为:3•2n-2n-3
1
2 3
4 6 5
8 12 10 7
16 24 20 14 9
32 48 40 28 19 11
…
可知每一列都是等比数列,每一行最后一个数是等差数列,公差为2,
所以第6类中的第2项是:3×24=48.
第n个类中n个数为:Sn=1×2 n-1+3×2n-2+5×2 n-3+…+(2n-1)•2 0…①
2Sn=1×2 n+3×2n-1+5×2 n-2+…+(2n-1)•2 1…②,
②-①得,Sn=2 n+2×2n-1+2×2 n-2+…+2•2 1-2n+1
=2 n+2n+2 n-1+…+2 2-2n+1
=2n+
| 4(1-2n-1) |
| 1-2 |
=3•2n-2n-348,
故答案为:3•2n-2n-3
点评:本题主要考查新定义和分析问题解决问题的能力,转化思想的应用,找出数列的特征是解题的关键.

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
设变量x,y满足约束条件
,则目标函数z=y-2x的最小值为( )
|
A、-
| ||
| B、-11 | ||
C、-
| ||
| D、3 |
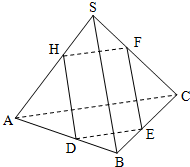 如图,在三棱锥S-ABC中,△ABC是边长为2的正三角形,SA=SB=SC=4,平面DEFH分别与三棱锥S-ABC的四条棱AB、BC、SC、SA交于D、E、F、H,若直线SB∥平面DEFH,直线AC∥平面DEFH,则平面DEFH与平面SAC所成的二面角(锐角)的余弦值等于
如图,在三棱锥S-ABC中,△ABC是边长为2的正三角形,SA=SB=SC=4,平面DEFH分别与三棱锥S-ABC的四条棱AB、BC、SC、SA交于D、E、F、H,若直线SB∥平面DEFH,直线AC∥平面DEFH,则平面DEFH与平面SAC所成的二面角(锐角)的余弦值等于