��Ŀ����
9������ͳ��ij�ָ�������Ķ��������y���ٽ��ÿĶʹ��ũ��1�ŷ���x��ǧ�ˣ�֮�������µĶ�Ӧ���ݣ�| x��ǧ�ˣ� | 2 | 4 | 5 | 6 | 8 |
| y���ٽ | 3 | 4 | 4 | 4 | 5 |
��2�����ݱ������ݣ�������С���˷����y����x�����Իع鷽��$\stackrel{��}{y}$=$\stackrel{��}{b}$x+$\stackrel{��}{a}$���������������Իع鷽�̣��������ÿĶʹ��ũ��1�ŷ���10ǧ�ˣ������ָ�������Ķ��������y�Ƕ��ٽ
�ο���ʽ��
1���ع鷽��ϵ����ʽ��$\stackrel{��}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$��$\stackrel{��}{a}$=$\overline{y}$-$\stackrel{��}{b}$$\overline{x}$
2.$\sum_{i=1}^{5}$xi2=145��$\sum_{i=1}^{5}$xiyi=106��
���� ��1����������5������д�ɶ�Ӧ�ĵ�����꣬������ϵ����������õ�ɢ��ͼ��
��2�����������������������������С���˷�����Ҫ�ļ������ݣ�������ϵ��b�Ĺ�ʽ����ý�����ٰ��������ĵ���룬���a��ֵ���õ����Իع鷽�̣���x=10�������Իع鷽�̣����ɵó����ۣ�
��� 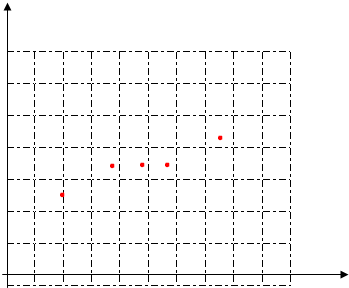 �⣺��1����ͼ-------------��3�֣�
�⣺��1����ͼ-------------��3�֣�
��2��$\overline{x}=\frac{2+4+5+6+8}{5}=5$----------------��4�֣�
$\overline{y}=\frac{3+4+4+4+5}{5}=4$---------------��5�֣�
$\sum_{i=1}^{5}{x}_{i}{y}_{i}$=106-----------------------��6�֣�
$\sum_{i=1}^5{{x_i}^2}={2^2}+{4^2}+{5^2}+{6^2}+{8^2}=145$----------------------------------------��7�֣�
$\hat b=\frac{106-5��5��4}{{145-5��{5^2}}}=0.3$----------------------------------------��8�֣�
$\hat a=\bar y-\hat b\overline{x}=4-0.3��5=2.5$-------------------------------------------��9�֣�
����y����x�����Իع鷽�̣�$\hat y=0.3x+2.5$------------------------------------��10�֣�
��x=10ʱ��$\hat y=0.3��10+2.5=5.5$---------------------------------------��11�֣�
�𣺹������ÿĶʹ��ũ��1�ŷ���10ǧ�ˣ������ָ�������Ķ��������y��550�-��12�֣�
���� ���⿼�����Իع鷽�̣���������֮��Ĺ�ϵ�����˺�����ϵ����������ع�ϵ��ͨ�������ع�ֱ�߷��̣��Ϳ��Ը����䲿�ֹ۲�ֵ����ö�����������֮�������ϵ���˽⣮

| A�� | ?x��0��x3��0 | B�� | $?{x_0}��0��x_0^3��0$ | C�� | ?x��0��x3��0 | D�� | $?{x_0}��0��x_0^3��0$ |
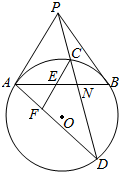 ��Բ��һ��P��ԲO������PA��PB��������PCD����C��PA��ƽ���ߣ��ֱ�AB��AD����E��F����֤��CE=EF��
��Բ��һ��P��ԲO������PA��PB��������PCD����C��PA��ƽ���ߣ��ֱ�AB��AD����E��F����֤��CE=EF��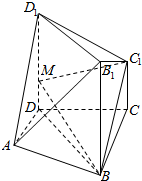 ��ͼ��������ABCD-B1C1D1�У�������BB1D1D��ƽ��ABCD��D1D��CC1��ƽ��D1DCC1����ƽ��B1BCC1���ɵĶ���ǵ�����ֵΪ$\frac{2}{3}$��BC=3��CD=2CC1=2��AD=$\sqrt{5}$��AD��BC��MΪDD1������һ�㣮
��ͼ��������ABCD-B1C1D1�У�������BB1D1D��ƽ��ABCD��D1D��CC1��ƽ��D1DCC1����ƽ��B1BCC1���ɵĶ���ǵ�����ֵΪ$\frac{2}{3}$��BC=3��CD=2CC1=2��AD=$\sqrt{5}$��AD��BC��MΪDD1������һ�㣮