题目内容
设数列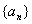 的前n项和为
的前n项和为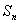 ,且
,且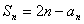 (
(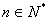 ).
).
(1)求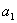 ,
,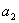 ,
,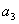 ,
,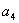 的值;
的值;
(2)猜想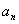 的表达式,并加以证明.
的表达式,并加以证明.
解:(1)因为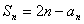 ,
, ,
,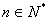
所以,当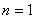 时,有
时,有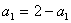 ,解得
,解得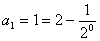 ;
;
当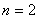 时,有
时,有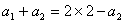 ,解得
,解得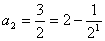 ;
;
当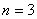 时,有
时,有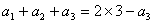 ,解得
,解得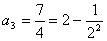 ;
;
当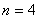 时,有
时,有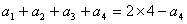 ,解得
,解得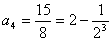 .
.
(2)猜想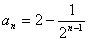 (
(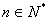 )
)
方法一:
由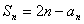 (
(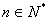 ),得
),得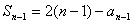 (
(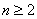 ),
),
两式相减,得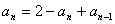 ,即
,即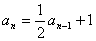 (
(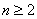 ).
).
两边减2,得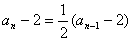 ,
,
所以{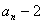 }是以-1为首项,
}是以-1为首项,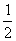 为公比的等比数列,
为公比的等比数列,
故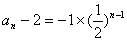 ,
,
即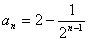 (
(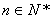 ).
).
方法二:
①当n=1时,由(1)可知猜想显然成立;
②假设当n=k时,猜想成立,即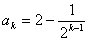 ,
,
由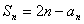 (
(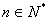 ),得
),得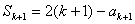 ,
,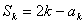
两式相减,得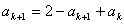 ,
,
所以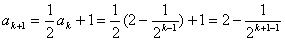 ,
,
即当n=k+1时,猜想也成立.
根据①和②,知对任意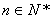 ,猜想成立.
,猜想成立.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
根据如下样本数据
| x | 3 | 4 | 5 | 6 | 7 |
| y | 4.0 | 2.5 |
| 0.5 |
|
得到的回归方程为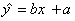 .若
.若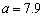 ,则
,则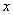 每增加1个单位,
每增加1个单位,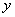 就 ( )
就 ( )
A.增加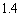 个单位; B.减少
个单位; B.减少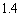 个单位; C.增加
个单位; C.增加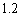 个单位; D.减少
个单位; D.减少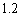 个单位.
个单位.

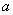 x-2在区间(1,+∞)内是增函数,则实数
x-2在区间(1,+∞)内是增函数,则实数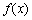 在定义域内可导,
在定义域内可导,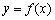 的图象如图1所示,则导函数
的图象如图1所示,则导函数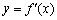 可能为 ( )
可能为 ( )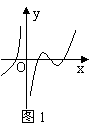
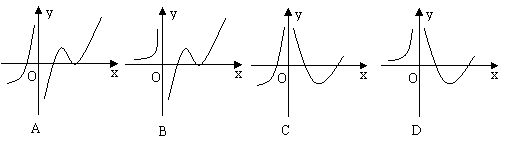
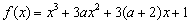 有极值,则
有极值,则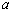 的取值范围是__
的取值范围是__ 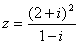 (i是虚数单位)在复平面上对应的点位于 ( )
(i是虚数单位)在复平面上对应的点位于 ( )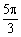 B.
B.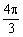 C.
C.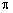 D.
D.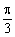

 0.5
0.5