题目内容
一个结晶体的形状为平行六面体,其中,以顶点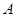 为端点的三条棱长都等于1,且它们彼此的夹角都是
为端点的三条棱长都等于1,且它们彼此的夹角都是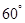 ,那么以这个顶点为端点的晶体的对角线的长为 。
,那么以这个顶点为端点的晶体的对角线的长为 。
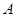 为端点的三条棱长都等于1,且它们彼此的夹角都是
为端点的三条棱长都等于1,且它们彼此的夹角都是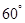 ,那么以这个顶点为端点的晶体的对角线的长为 。
,那么以这个顶点为端点的晶体的对角线的长为 。
由 平方得
平方得
 平方得
平方得

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
题目内容
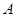 为端点的三条棱长都等于1,且它们彼此的夹角都是
为端点的三条棱长都等于1,且它们彼此的夹角都是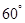 ,那么以这个顶点为端点的晶体的对角线的长为 。
,那么以这个顶点为端点的晶体的对角线的长为 。
 平方得
平方得

 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案