题目内容
20.过抛物线$y=\frac{1}{4}{x^2}$的焦点的直线与抛物线交于A,B两点,O是抛物线的顶点.(1)判断抛物线的准线和以AB为直径的圆的位置关系;
(2)求$\overrightarrow{OA}•\overrightarrow{OB}$的值.
分析 (1)取AB的中点M,分别过A、B、M作准线的垂线AP、BQ、MN,垂足分别为P、Q、N,作出图形,利用抛物线的定义及梯形的中位线性质可推导,|MN|=$\frac{1}{2}$|AB|,从而可判断圆与准线的位置关系.
(2)由抛物线x2=4y与过其焦点(0,1)的直线方程联立,消去y整理成关于x的一元二次方程,设出A(x1,y1)、B(x2,y2)两点坐标,$\overrightarrow{OA}•\overrightarrow{OB}$=x1•x2+y1•y2,由韦达定理可以求得答案.
解答  解:(1)取AB的中点M,分别过A、B、M作准线的垂线AP、BQ、MN,垂足分别为P、Q、N,如图所示:
解:(1)取AB的中点M,分别过A、B、M作准线的垂线AP、BQ、MN,垂足分别为P、Q、N,如图所示:
由抛物线的定义可知,|AP|=|AF|,|BQ|=|BF|,
在直角梯形APQB中,|MN|=$\frac{1}{2}$(|AP|+|BQ|)=$\frac{1}{2}$(|AF|+|BF|)
=$\frac{1}{2}$|AB|,
故圆心M到准线的距离等于半径,
所以以AB为直径的圆与抛物线的准线相切.
(2)由题意知,抛物线x2=4y的焦点坐标为(0,1),∴直线AB的方程为y-1=kx,即y=kx+1
由$\left\{\begin{array}{l}{x}^{2}=4y\\ y=kx+1\end{array}\right.$得x2-4kx-4=0,设A(x1,y1),B(x2,y2),x1+x2=4k,x1x2=-4,
则,y1•y2=(kx1+1)•(kx2+1)=k2x1•x2+k(x1+x2)+1=1.
∴$\overrightarrow{OA}•\overrightarrow{OB}$=x1•x2+y1•y2=1-4=-3,
点评 本题考查直线与圆锥曲线的关系,解决问题的关键是联立抛物线方程与过其焦点的直线方程,利用韦达定理予以解决,抛物线过焦点弦的性质,关键是正确运用抛物线的定义,合理转化,综合性强.

 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案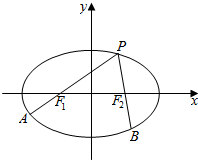 如图,F1F2为椭圆C:$\frac{{x}^{2}}{4}$$+\frac{{y}^{2}}{3}$=1的左、右焦点,点P为椭圆C上一点,延长PF1、,PF2分别交椭圆C于A,B.若$\overrightarrow{P{F}_{1}}$=2$\overrightarrow{{F}_{1}A}$,$\overrightarrow{P{F}_{2}}$=$λ\overrightarrow{{F}_{2}B}$,则λ=( )
如图,F1F2为椭圆C:$\frac{{x}^{2}}{4}$$+\frac{{y}^{2}}{3}$=1的左、右焦点,点P为椭圆C上一点,延长PF1、,PF2分别交椭圆C于A,B.若$\overrightarrow{P{F}_{1}}$=2$\overrightarrow{{F}_{1}A}$,$\overrightarrow{P{F}_{2}}$=$λ\overrightarrow{{F}_{2}B}$,则λ=( )| A. | 1 | B. | $\sqrt{2}$ | C. | $\frac{4}{3}$ | D. | $\frac{5}{4}$ |
| A. | $\frac{1}{2}$+$\frac{\sqrt{2}}{2}$ | B. | 1+$\frac{\sqrt{2}}{2}$ | C. | 1+$\sqrt{2}$ | D. | 2+$\sqrt{2}$ |
| A. | $\frac{{\sqrt{3}}}{4}$ | B. | $\frac{{\sqrt{2}}}{4}$ | C. | $\frac{{\sqrt{2}}}{8}$ | D. | $\frac{{\sqrt{3}}}{8}$ |
| A. | {5} | B. | {2} | C. | {1,2,3,4} | D. | {1,3,4,5} |