Question

【题目】如图， 是圆柱的母线， 是的直径， 是底面圆周上异于的任意一点， ， .

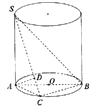
（1）求证：

（2）当三棱锥的体积最大时，求与平面所成角的大小；

（3）上是否存在一点，使二面角的平面角为45°？若存在，求出此时的长；若不存在，请说明理由.

Answer 1

【答案】（1）证明见解析；（2）45°；（3）存在这样的点且，证明见解析.

【解析】试题分析：（1）平面平面， ，所以平面， ；（2）时，三棱锥体积的最大， 与平面所成角度为45°；（3）存在这样的点且。

试题解析：

（1）∵平面， 平面

∴，又，

∴平面

又∵平面，

∴平面平面，

而平面平面，

∴平面，而平面，

∴

（2）设，在中，

∵平面，

∴是三棱锥的高

因此三棱锥的体积为

∵， ，

∴当，即时，三棱锥体积的最大值为

此时为等腰直角三角形，

∴与平面所成角度为45°

（3）存在这样的点且，理由如下：

记的中点为，连接，

∵为等腰直角三角形

∴，由（1）知，

∴平面，

又平面，∴

∴是二面角的平面角，即

为等腰直角三角形， ，

∴

在中，

在和中，可解得，