Question

【题目】将名学生分成两组参加城市绿化活动，其中组布置盆盆景， 组种植棵树苗.根据历年统计，每名学生每小时能够布置盆盆景或者种植棵树苗.设布置盆景的学生有人，布置完盆景所需要的时间为，其余学生种植树苗所需要的时间为（单位：小时，可不为整数）.

⑴写出、的解析式；

⑵比较、的大小，并写出这名学生完成总任务的时间的解析式；

⑶应怎样分配学生，才能使得完成总任务的时间最少？

Answer 1

【答案】（1）， ， ；（2）见解析；（3）布置盆景和种植树苗的学生分别有人或人.

【解析】试题分析：（1）设布置盆景的学生有x人，则B组人数为51-x，可求出A组所用时间， ， ，化简即可；
（2）通过作差比较g（x）、h（x）的大小，确定A组与B组的所需时间，写出分段函数的解析式即可．
（3）通过两组用时比较，计算x=20与x=21时，求出总用时最少者，即可得到结果．

试题解析：

⑴由题意布置盆景的学生有人，种植树苗的学生有人，所以， .

， ；

⑵，因为所以

当时，

当时，

所以；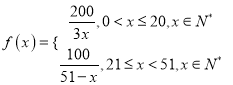

⑶完成总任务所用时间最少即求的最小值

当时， 递减，则.

故的最小值为，此时人

当时， 递增，则

故的最小值为，此时人

所以布置盆景和种植树苗的学生分别有人或人.