题目内容
4.已知向量$\overrightarrow{a}$=(3,-2),$\overrightarrow{b}$=(x,y-1)且$\overrightarrow{a}$∥$\overrightarrow{b}$,若x,y均为正数,则$\frac{3}{x}$+$\frac{2}{y}$的最小值是( )| A. | 24 | B. | 8 | C. | $\frac{8}{3}$ | D. | $\frac{5}{3}$ |
分析 根据向量共线定理列出方程,得出2x+3y=3,再求$\frac{3}{x}+\frac{2}{y}$的最小值即可.
解答 解:∵$\overrightarrow a$∥$\overrightarrow b$,
∴-2x-3(y-1)=0,
化简得2x+3y=3,
∴$\frac{3}{x}+\frac{2}{y}$=($\frac{3}{x}$+$\frac{2}{y}$)×$\frac{1}{3}$(2x+3y)
=$\frac{1}{3}$(6+$\frac{9y}{x}$+$\frac{4x}{y}$+6)≥$\frac{1}{3}$(12+2$\sqrt{\frac{9y}{x}•\frac{4x}{y}}$)=8,
当且仅当2x=3y=$\frac{3}{2}$时,等号成立;
∴$\frac{3}{x}+\frac{2}{y}$的最小值是8.
故选:B.
点评 本题考查了平面向量的共线定理与基本不等式的应用问题,是综合性题目.

练习册系列答案
相关题目
15.若$θ∈(\frac{π}{4},\frac{π}{2}),sin2θ=\frac{1}{16}$,则cosθ-sinθ的值是( )
| A. | $\frac{{\sqrt{15}}}{4}$ | B. | $-\frac{{\sqrt{15}}}{4}$ | C. | $\frac{1}{4}$ | D. | $-\frac{1}{4}$ |
19.设集合A={x|$\frac{x-2}{x+1}$<0},B={x|y=$\sqrt{1-{x}^{2}}$},则A∩B=( )
| A. | {x|-1<x≤1} | B. | {x|-1<x<1} | C. | {x|-1≤x<1} | D. | {-1,1} |
9.已知Z=$\frac{2i}{1+i}$(i为虚数单位),则Z的共轭复数在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
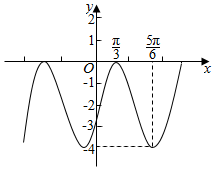 已知函数f(x)=sinωx(sinωx+2$\sqrt{3}$cosωx)+sin(ωx-$\frac{π}{4}$)sin(ωx+$\frac{π}{4}$)(其中ω为常数,且ω>0),函数g(x)=f(x)-$\frac{5}{2}$的部分图象如图所示.
已知函数f(x)=sinωx(sinωx+2$\sqrt{3}$cosωx)+sin(ωx-$\frac{π}{4}$)sin(ωx+$\frac{π}{4}$)(其中ω为常数,且ω>0),函数g(x)=f(x)-$\frac{5}{2}$的部分图象如图所示.