题目内容
数列{an}满足a1=1,anan+1=4n(n∈N*),则a2+a4+…+a2n= .
考点:数列的求和
专题:等差数列与等比数列
分析:根据数列的递推关系得到数列{a2n}是首项为a2,公比q=4的等比数列,利用等比数列的前n项和公式即可得到结论.
解答:
解:∵a1=1,anan+1=4n(n∈N*),
∴an+1an+2=4n+1(n∈N*),
两式相除得
=
=4,
即数列{a2n}是首项为a2,公比q=4的等比数列,
当n=1时,a1a2=4,则a2=4,
则a2+a4+…+a2n=
=
(4n-1),
故答案为:
(4n-1)
∴an+1an+2=4n+1(n∈N*),
两式相除得
| an+2 |
| an |
| 4n+1 |
| 4n |
即数列{a2n}是首项为a2,公比q=4的等比数列,
当n=1时,a1a2=4,则a2=4,
则a2+a4+…+a2n=
| 4(1-4n) |
| 1-4 |
| 4 |
| 3 |
故答案为:
| 4 |
| 3 |
点评:本题主要考查数列的求和,根据条件求出数列{a2n}是首项为a2,公比q=4的等比数列是解决本题的关键.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
相关题目
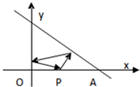 如图,已知A(4,0)、B(0,4),从点P(2,0)射出的光线经直线AB反射后再射到直线OB上,最后经直线OB反射到P点.求(1)光线所经过的路程是多少;(2)直线AB关于直线2x-y-2=0的对称直线.
如图,已知A(4,0)、B(0,4),从点P(2,0)射出的光线经直线AB反射后再射到直线OB上,最后经直线OB反射到P点.求(1)光线所经过的路程是多少;(2)直线AB关于直线2x-y-2=0的对称直线.