如果不等式|x-1|+|x+2|＞ax的解集是R.求实数a的取值范围．题目和参考答案——青夏教育精英家教网—

题目内容

14．如果不等式|x-1|+|x+2|＞ax（a＞0）的解集是R，求实数a的取值范围．

分析令f（x）=|x-1|+|x+2|=$\left\{\begin{array}{l}{-1-2x，x＜-2}\\{3，-2≤x≤1}\\{2x+1，x＞1}\end{array}\right.$，则由题意可得函数f（x）的图象恒在函数g（x）的图象的上方，数形结合求得a的范围．

解答解：令f（x）=|x-1|+|x+2|=$\left\{\begin{array}{l}{-1-2x，x＜-2}\\{3，-2≤x≤1}\\{2x+1，x＞1}\end{array}\right.$，g（x）=ax，图象如图所示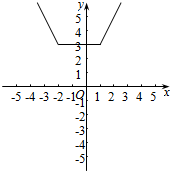

∴不等式|x-1|+|x+2|＞ax（a＞0）的解集是R，
∴0＜a≤2．

点评本题主要考查带有绝对值的函数，函数的恒成立问题，体现了转化、数形结合的数学思想，属于中档题．

练习册系列答案

相关题目

（Ⅰ）图中①②分别填什么？
（Ⅱ）求输出值S的结果．（要求写出解题过程，求出最后的结果）

7．已知sinα=$\frac{1}{5}$+cosα，且$α∈（0，\frac{π}{2}）$，则$\frac{{\sqrt{2}cos（α+\frac{π}{4}）}}{cos2α}$的值为$\frac{5}{7}$．

2．已知角A、B、C为△ABC的三个内角，其对边分别为a、b、c，若a²=b²+c²+bc，且a=2$\sqrt{3}$．
（Ⅰ）若△ABC的面积S=$\sqrt{3}$，求b+c的值；
（Ⅱ）求b+c的取值范围．

9．已知数列{a_n}满足a_n＞0，且a_n=$\frac{2{a}_{n+1}}{1-{{a}_{n+1}}^{2}}$（n∈N^*）．
（1）证明：a_n+1＜$\frac{1}{2}$a_n（n∈N^*）；
（2）令b_n=-a_n+1²+a_na_n+1（n∈N^*），数列{b_n}的前n项和为T_n，求证：T_n＜$\frac{1}{3}$a₁²．

18．若函数f（x）为R上的奇函数，且当x＜0时，f（x）=-x²-1，则当x∈R时，f（x）=$\left\{\begin{array}{l}-{x}^{2}-1，x＜0\\ 0，x=0\\{x}^{2}+1，x＞0\end{array}\right.$．

5．已知全集U={x∈Z|x²-3x-10＜0}，集合P={0，3}，Q=|2，0，1}，则∁_U（P∪Q）=（　　）

2．若a+a^-1=7，则a${\;}^{\frac{1}{2}}$+a${\;}^{-\frac{1}{2}}$=3．

2．圆台的上、下底面半径分别为R，r，求该圆台的内切球的半径．

试题分类