题目内容
17.下列说法中正确的个数是( )①命题“若a=0,则ab=0”的否命题是:“若a=0,则ab≠0”;
②命题p:“?x∈(-∞,0),2x<3x”,则¬p:“?x∈[0,+∞),2x≥3x”;
③对于实数a,b,“b<a<0”是“$\frac{1}{b}$>$\frac{1}{a}$”成立的充分不必要条件
④如果命题“¬p”与命题“p或q”都是真命题,那么命题q一定是真命题.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 ①命题“若a=0,则ab=0”的否命题是:“若a≠0,则ab≠0”,即可判断出正误;
②利用非命题的定义即可判断出正误;
③对于实数a,b,“b<a<0”⇒“$\frac{1}{b}$>$\frac{1}{a}$”,反之不成立,例如取a>b>0时,$\frac{1}{b}$>$\frac{1}{a}$,即可判断出正误;
④由已知可得:可得命题p是假命题,q一定是真命题,即可判断出正误.
解答 解:①命题“若a=0,则ab=0”的否命题是:“若a≠0,则ab≠0”,因此不正确;
②命题p:“?x∈(-∞,0),2x<3x”,则¬p:“?x∈(-∞,0),2x≥3x”,不正确;
③对于实数a,b,“b<a<0”⇒“$\frac{1}{b}$>$\frac{1}{a}$”,反之不成立,例如取a>b>0时,$\frac{1}{b}$>$\frac{1}{a}$,因此,“b<a<0”是“$\frac{1}{b}$>$\frac{1}{a}$”成立的充分不必要条件,正确;
④如果命题“¬p”与命题“p或q”都是真命题,那么命题p是假命题,q一定是真命题,正确.
综上可得:正确的命题个数为2.
故选:B.
点评 本题考查了简易逻辑的判定方法、不等式的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
2.设等比数列{an}的公比q=2,前n项和为Sn,则$\frac{S_3}{a_3}$的值为( )
| A. | $\frac{15}{4}$ | B. | $\frac{15}{2}$ | C. | $\frac{7}{4}$ | D. | $\frac{7}{2}$ |
9.函数y=log3(3-x)的定义域为( )
| A. | (-∞,3] | B. | (-∞,3) | C. | (3,+∞) | D. | [3,+∞) |
6.已知复数z=1-i,则$\frac{z-1}{{z}^{2}}$=( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{1}{2}$i | D. | $\frac{1}{2}$i |
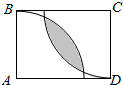 如图在矩形ABCD,AB=1,AD=$\sqrt{2}$,在矩形区域内任取一点P,使得该点落在阴影部分内的概率为$\frac{\sqrt{2}π}{6}-\frac{\sqrt{6}}{4}$.
如图在矩形ABCD,AB=1,AD=$\sqrt{2}$,在矩形区域内任取一点P,使得该点落在阴影部分内的概率为$\frac{\sqrt{2}π}{6}-\frac{\sqrt{6}}{4}$.