题目内容
已知函数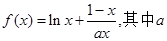 为大于零的常数。
为大于零的常数。
(1)若函数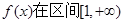 内调递增,求a的取值范围;
内调递增,求a的取值范围;
(2)求函数 在区间[1,2]上的最小值。
在区间[1,2]上的最小值。
(1) ,(2)①当
,(2)①当
②当 时,
时,
③当
解析试题分析: 2分
2分
(1)由已知,得 上恒成立, 3分
上恒成立, 3分
即 上恒成立, 又
上恒成立, 又 当
当 5分
5分 6分
6分
(2)①当 时,
时, 在(1,2)上恒成立, 这时
在(1,2)上恒成立, 这时 在[1,2]上为增函数
在[1,2]上为增函数 8分
8分
②当
 在(1,2)上恒成立, 这时
在(1,2)上恒成立, 这时 在[1,2]上为减函数
在[1,2]上为减函数 10分
10分
③当 时, 令
时, 令
又

 12分
12分
综上, 在[1,2]上的最小值为
在[1,2]上的最小值为
①当
②当 时,
时,
③当 13分
13分
考点:本题考查了导数的运用
点评:对于此类问题要把函数的单调性特征与导数两个知识加以有机会组合.特别,在研究函数的单调区间或决断函数的单调性时,三个基本步骤不可省,一定要在定义域内加以求解单调区间或判断单调性

练习册系列答案
相关题目
 +
+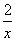 在
在 1,+∞)上是单调函数,求实数a的取值范围.
1,+∞)上是单调函数,求实数a的取值范围. 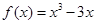
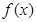 的单调区间;(2)求
的单调区间;(2)求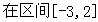 上的最小值.
上的最小值. (
(
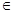 R).
R).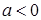 ,求函数
,求函数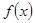 的极值;
的极值;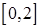 上有两个零点,若存在,求出
上有两个零点,若存在,求出 ,
,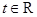 .
.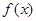 的极值点;
的极值点; 对
对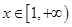 恒成立,求实数
恒成立,求实数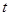 的取值范围.
的取值范围.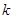 和
和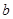 ,使得函数
,使得函数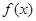 和
和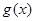 对其定义域上的任意实数
对其定义域上的任意实数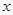 分别满足:
分别满足: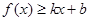 和
和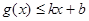 ,则称直线
,则称直线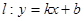 为
为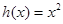 ,
,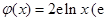 为自然对数的底数).
为自然对数的底数).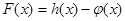 的极值;
的极值; 和
和 是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.
是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由. .
. 时,求证:函数
时,求证:函数 在
在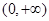 上单调递增;
上单调递增;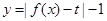 有三个零点,求
有三个零点,求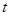 的值.
的值.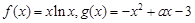 .
.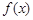 在
在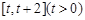 上的最小值;
上的最小值;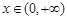 ,
,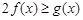 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.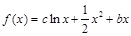
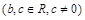 ,且
,且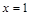 为
为 的极值点.
的极值点.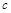 表示);
表示);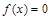 恰有两解,求实数
恰有两解,求实数