题目内容
(本题满分14分)设函数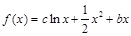
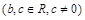 ,且
,且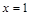 为
为 的极值点.
的极值点.
(Ⅰ) 若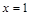 为
为 的极大值点,求
的极大值点,求 的单调区间(用
的单调区间(用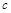 表示);
表示);
(Ⅱ) 若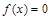 恰有两解,求实数
恰有两解,求实数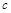 的取值范围.
的取值范围.
解析试题分析:解: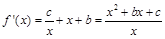 ,又
,又 ,则
,则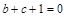 ,
,
所以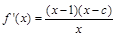 且
且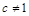 , 3分
, 3分
(Ⅰ)因为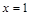 为
为 的极大值点,所以
的极大值点,所以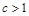 .
.
令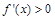 ,得
,得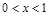 或
或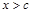 ;令
;令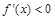 ,得
,得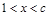 .
.
所以 的递增区间为
的递增区间为 ,
,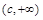 ;递减区间为
;递减区间为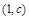 . 6分
. 6分
(Ⅱ)①若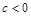 ,则
,则 在
在 上递减,在
上递减,在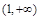 上递增.
上递增.
若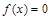 恰有两解,则
恰有两解,则 ,即
,即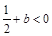 ,所以
,所以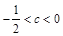 . 8分
. 8分
②若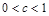 ,则
,则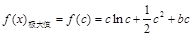 ,
,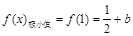 .
.
因为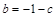 ,则
,则 ,
,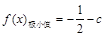 ,从而
,从而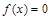 只有一解; 10分
只有一解; 10分
③若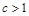 ,则
,则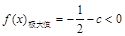 ,
,
从而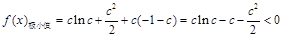 ,
,
则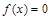 只有一解. 12分
只有一解. 12分
综上,使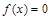 恰有两解的
恰有两解的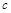 的范围为
的范围为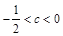 14分
14分
考点:本题考查导数的应用,分类讨论思想,考查运算求解能力、逻辑思维能力和分析问题解决问题的能力,较难题.
点评:

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
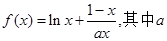 为大于零的常数。
为大于零的常数。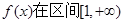 内调递增,求a的取值范围;
内调递增,求a的取值范围; 在区间[1,2]上的最小值。
在区间[1,2]上的最小值。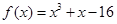 .
.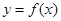 在点
在点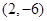 处的切线方程;
处的切线方程; 为曲线
为曲线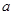 为实数,函数
为实数,函数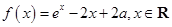 。
。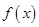 的单调区间与极值;
的单调区间与极值;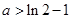 且
且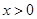 时,
时,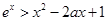 。
。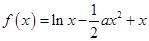 ,
, R.
R. 的单调区间;
的单调区间;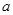 ,使得函数
,使得函数 ?若存在,求
?若存在,求 (2)
(2)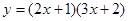
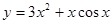 (4)
(4)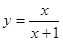
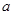 是实数,函数
是实数,函数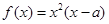 。
。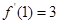 ,求
,求 在点
在点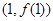 处的切线方程;
处的切线方程;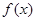 在区间
在区间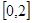 上的最大值。
上的最大值。 (a>0,b,cÎR),曲线
(a>0,b,cÎR),曲线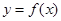 在点P(0,f (0))处的切线方程为
在点P(0,f (0))处的切线方程为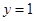 .
.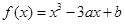 在
在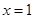 处有极小值
处有极小值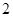 。
。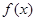 的解析式;
的解析式;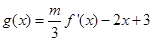 在
在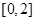 只有一个零点,求
只有一个零点,求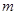 的取值范围。
的取值范围。