Question

①求由曲线y=

x

，直线y=2-x，y=-

1

3

x围成的图形的面积．
②求由y=sinx，直线x=

π

2

，x=π，x轴围成的区域绕x轴旋转一周所得几何体的体积？

Answer 1

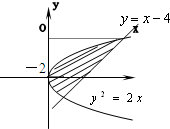
①区域对应的图形如图：
由

y= x y=2-x

．解得x=1或x=4（舍去），即A点的横坐标为1，
由

y=2-x y=- 1 3 x

，解得x=3，BA点的横坐标为3，
∴所求区域的面积为

∫

10

[

x

-(-

1

3

x)]dx+

∫

31

[2-x-(-

1

3

x)]dx
=（

2

3

x

3

2

+

1

6

x2）|

10

+（2x-

1

3

x2）|

31

=

2

3

+

1

6

+(2×3-

1

3

×32-2+

1

3

)=2+

1

6

=

13

6

．
②根据旋转体的体积公式可知所求体积为V=

∫

π π 2

(sin2x)dx=

∫

π π 2

(

1-cos2x

2

)dx=

∫

π π 2

1

2

dx+

1

2

∫

π π 2

cos2xdx
=

1

2

x|

π π 2

+

1

2

×

1

2

sin2x|

π π 2

=

1

2

×(π-

π

2

)+

1

4

(sin2π-sinπ)=

1

2

×

π

2

=

π

4

．