Question

【题目】△ABC的内角A，B，C的对边分别为a，b，c.已知asin（A+B）＝csin.

（1）求A；

（2）求sinBsinC的取值范围；

（3）若△ABC的面积为，周长为8，求a.

Answer 1

【答案】（1）A（2）（0，）（3）a

【解析】

（1）用诱导公式和正弦定理化边为角，然后再由二倍角公式变形后可求得；

（2）由（1）可得，，把化为的函数，由三角函数恒等变换化为一个三角函数形式，结合正弦函数性质可得取值范围；

（3）由三角形面积可求得，由周长及余弦定理得的三个等式，消去可解得．

（1）△ABC中，asin（A+B）＝csin，

∴asin（π﹣C）＝csin（），

∴asinC＝ccos，由正弦定理得sinAsinC＝sinCcos，

∴sinA＝cos，即2sincoscos；

又A∈（0，π），

∴cos0，

∴2sin1，即sin，

∴，

解得A；

（2）∵sinBsinC＝sinBsin（B）sinBcosBsin2Bsin2Bcos2Bsin（2B），

又∵B∈（0，），

∴2B∈（，），sin（2B）∈（，1]，

∴sinBsinC∈（0，）.

（3）△ABC的面积为，周长为8，

∴bcsinAbc，

∴bc＝4，…①

a+b+c＝8，…②

由余弦定理得：a2＝b2+c2﹣bc，…③

由①②③组成方程组，可得：，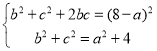

可得：（8﹣a）2＝a2+12，

解得：a.