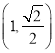题目内容
【题目】如图，在直三棱柱ABC-A1B1C1中，D，E分别为AB，BC的中点，点F在侧棱B1B上，且
， 
.
求证：（1）直线DE
平面A1C1F；
（2）平面B1DE⊥平面A1C1F.
【答案】（1）详见解析（2）详见解析
【解析】试题（1）利用线面平行判定定理证明线面平行，而线线平行的寻找往往结合平面几何的知识，如中位线的性质等；（2）利用面面垂直判定定理证明，即从线面垂直出发给予证明，而线面垂直的证明，往往需要多次利用线面垂直性质定理与判定定理.
试题解析：证明：（1）在直三棱柱
中， 
在三角形ABC中，因为D，E分别为AB，BC的中点，
所以
，于是
，
又因为DE
平面
平面
，
所以直线DE//平面
.
（2）在直三棱柱
中， 
因为
平面
，所以
，
又因为
，
所以
平面
.
因为
平面
，所以
.
又因为
，
所以
.
因为直线
，所以
【题目】《中国好声音（
）》是由浙江卫视联合星空传媒旗下灿星制作强力打造的大型励志专业音乐评论节目，于2012年7月13日在浙江卫视播出.每期节目有四位导师参加.导师背对歌手，当每位参赛选手演唱完之前有导师为其转身，则该选手可以选择加入为其转身的导师的团队中接受指导训练.已知某期《中国好声音》中，6位选手唱完后，四位导师为其转身的情况如下表所示：
导师转身人数（人） | 4 | 3 | 2 | 1 |
获得相应导师转身的选手人数（人） | 1 | 2 | 2 | 1 |
现从这6位选手中随机抽取两人考查他们演唱完后导师的转身情况.
（1）求选出的两人导师为其转身的人数和为4的概率；
（2）记选出的2人导师为其转身的人数之和为
，求
的分布列及数学期望
.
【题目】随着科学技术的飞速发展，手机的功能逐渐强大，很大程度上代替了电脑、电视．为了了解某高校学生平均每天使用手机的时间是否与性别有关，某调查小组随机抽取了
名男生、
名女生进行为期一周的跟踪调查，调查结果如表所示：
平均每天使用手机超过 | 平均每天使用手机不超过 | 合计 | |
男生 |
|
|
|
女生 |
|
|
|
合计 |
|
|
|
（1）能否在犯错误的概率不超过
的前提下认为学生使用手机的时间长短与性别有关？
（2）在这
名女生中，调查小组发现共有
人使用国产手机，在这
人中，平均每天使用手机不超过
小时的共有
人．从平均每天使用手机超过
小时的女生中任意选取
人，求这
人中使用非国产手机的人数
的分布列和数学期望．
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
参考公式： 
