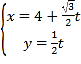题目内容
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,以原点为圆心,椭圆
,以原点为圆心,椭圆![]() 的短半轴长为半径的圆与直线
的短半轴长为半径的圆与直线![]() 相切.
相切.
(Ⅰ)求椭圆方程;
(Ⅱ)设![]() 为椭圆右顶点,过椭圆
为椭圆右顶点,过椭圆![]() 的右焦点的直线
的右焦点的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点(异于
两点(异于![]() ),直线
),直线![]() ,
,![]() 分别交直线
分别交直线![]() 于
于![]() ,
,![]() 两点. 求证:
两点. 求证:![]() ,
,![]() 两点的纵坐标之积为定值.
两点的纵坐标之积为定值.
【答案】(Ⅰ)![]() ;(Ⅱ)详见解析.
;(Ⅱ)详见解析.
【解析】
(Ⅰ)求出![]() 后可得椭圆方程.
后可得椭圆方程.
(Ⅱ)当直线![]() 的斜率不存在,计算可得
的斜率不存在,计算可得![]() 两点的纵坐标之积为
两点的纵坐标之积为![]() .当直线
.当直线![]() 的斜率存在时,可设直线
的斜率存在时,可设直线![]() 的方程为
的方程为![]() ,
,![]() ,则
,则![]() ,联立直线方程和椭圆方程,消去
,联立直线方程和椭圆方程,消去![]() 后利用韦达定理化简
后利用韦达定理化简![]() 后可得定值.
后可得定值.
解:(Ⅰ)因为以原点为圆心,椭圆的短半轴长为半径的圆与直线![]() 相切,
相切,
所以半径![]() 等于原点到直线的距离
等于原点到直线的距离![]() ,
, ,即
,即![]() .
.
由离心率![]() ,可知
,可知![]() ,且
,且![]() ,得
,得![]() .
.
故椭圆![]() 的方程为
的方程为![]() .
.
(Ⅱ)由椭圆![]() 的方程可知
的方程可知![]() .
.
若直线![]() 的斜率不存在,则直线
的斜率不存在,则直线![]() 方程为
方程为![]() ,
,
所以![]() .
.
则直线![]() 的方程为
的方程为![]() ,直线
,直线![]() 的方程为
的方程为![]() .
.
令![]() ,得
,得![]() ,
,![]() .
.
所以![]() 两点的纵坐标之积为
两点的纵坐标之积为![]() .
.
若直线![]() 的斜率存在,设直线
的斜率存在,设直线![]() 的方程为
的方程为![]() ,
,
由![]() 得
得![]() ,
,
依题意![]() 恒成立.
恒成立.
设![]() ,
,
则![]() .
.
设![]()
![]() ,
,
由题意![]() 三点共线可知
三点共线可知![]() ,
,
所以点![]() 的纵坐标为
的纵坐标为![]() .同理得点
.同理得点![]() 的纵坐标为
的纵坐标为![]() .
.
所以![]()
![]()
![]()
![]()
![]()
综上,![]() 两点的纵坐标之积为定值.
两点的纵坐标之积为定值.

 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案【题目】已知甲、乙两地生产同一种瓷器,现从两地的瓷器中随机抽取了一共300件统计质量指标值,得到如图的两个统计图,其中甲地瓷器的质量指标值在区间![]() 和
和![]() 的频数相等.
的频数相等.

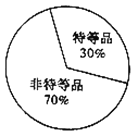
甲地瓷器质量频率分布直方图 乙地瓷器质量扇形统计图
(1)求直方图中![]() 的值,并估计甲地瓷器质量指标值的平均值;(同一组中的数据用区间的中点值作代表)
的值,并估计甲地瓷器质量指标值的平均值;(同一组中的数据用区间的中点值作代表)
(2)规定该种瓷器的质量指标值不低于125为特等品,且已知样本中甲地的特等品比乙地的特等品多10个,结合乙地瓷器质量扇形统计图完成下面的![]() 列联表,并判断是否有95%的把握认为甲、乙两地的瓷器质量有差异?
列联表,并判断是否有95%的把握认为甲、乙两地的瓷器质量有差异?
物等品 | 非特等品 | 合计 | |
甲地 | |||
乙地 | |||
合计 |
附: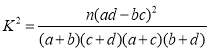 ,其中
,其中![]() .
.
| 0.10 | 0.05 | 0.025 | 0.01 |
| 2.706 | 3.841 | 5.024 | 6.635 |