Question

变量x，y满足

x-4y+3≤0 3x+5y-25≤0 x≥1

（1）设z=

y

x

，求z的最小值；
（2）设z=x²+y²+6x-4y+13，求z的取值范围．

Answer 1

考点：简单线性规划

专题：函数的性质及应用

分析：（1）先画出满足条件的平面区域，求出A，B，C的坐标，根据z=

y

x

的几何意义，从而求出z的最小值；
（2）z=（x+3）²+（y-2）²的几何意义是可行域上的点到点（-3，2）的距离的平方，结合图形求出即可．

解答： 解　由约束条件

x-4y+3≤0 3x+5y-25≤0 x≥1

作出（x，y）的可行域，
如图阴影部分所示：

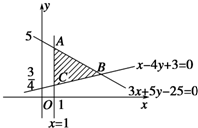
由

x=1 3x+5y-25=0

，解得A（1，

22

5

），
由

x=1 x-4y+3=0

，解得C（1，1），
由

x-4y+3=0 3x+5y-25=0

，可得B（5，2），
（1）∵z=

y

x

=

y-0

x-0

，
∴z的值即是可行域中的点与原点O连线的斜率，
观察图形可知z_min=k_OB=

2

5

；
（2）z=x²+y²+6x-4y+13=（x+3）²+（y-2）²的几何意义是可行域上的点到点（-3，2）的距离的平方，
结合图形可知，可行域上的点到（-3，2）的距离中，
d_min=4，d_max=8．
故z的取值范围是[16，64]．

点评：本题考查了线性规划问题，考查了数形结合思想，是一道中档题．