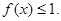题目内容
已知函数![]() R).
R).
(1)若![]() 在
在![]() 时取得极值,求
时取得极值,求![]() 的值;
的值;
(2)求![]() 的单调区间;
的单调区间;
(3)求证:当![]() 时,
时,![]() .
.
同下
解析:
(1)![]() ,
,![]() 是一个极值点,
是一个极值点,![]() ,
,![]() .(3分)
.(3分)
此时![]() .
.
![]() 的定义域是
的定义域是![]() ,
,
![]() 当
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
![]() 当
当![]() 时,
时,![]() 是
是![]() 的极小值点,
的极小值点,![]() .(5分)
.(5分)
(2)![]()
![]() 当
当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() .(7分)
.(7分)
当![]() 时,
时,![]() ,
,
令![]() 有
有![]() ,
,![]() 函数
函数![]() 的单调递增区间为
的单调递增区间为![]() ;
;
令![]() 有
有![]() ,
,![]() 函数
函数![]() 的单调递减区间为
的单调递减区间为![]() .(10分)
.(10分)
(3)设![]() ,
,![]() ,
,
![]() 当
当![]() 时,
时,![]() ,
,
![]() 在
在![]() 上是增函数,
上是增函数,![]()
![]() ,
,
![]() 当
当![]() 时,
时,![]() (15分)
(15分)

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
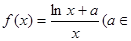 R).
R).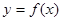 在点
在点 处的切线与直线
处的切线与直线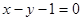 平行,求
平行,求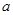 的值;
的值;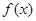 的单调区间和极值;
的单调区间和极值;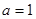 ,且
,且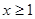 时,证明:
时,证明: